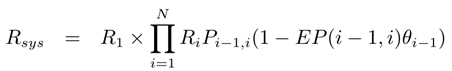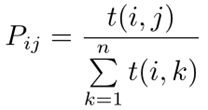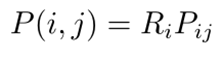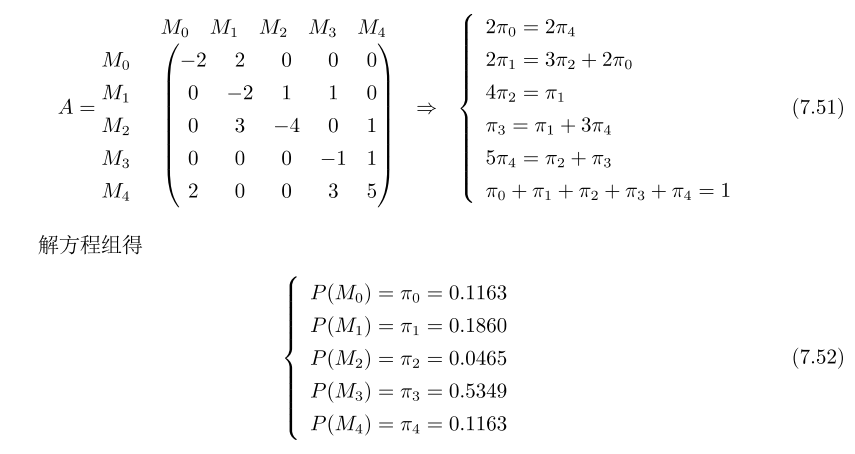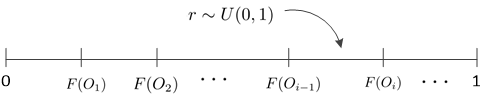本文最后更新于:2025年2月2日 晚上
软件可靠性复习
2.软件可靠性基本概念
软件可靠性定义:在规定的条件下和规定的时间内,软件不引起系统失效的概率。
规定的条件:运行环境(硬件、操作系统、输入格式、输入范围等)、操作剖面(输入空间及其概率分布)
2.1可靠性度量指标(计算)
-
可靠度R(t)
设T表示从软件运行开始(t=0)到软件失效所经历的时间,则在时刻t的软件可靠度R(t)=P{T>t}
-
不可靠度F(t)(失效分布函数、累计失效概率)
F(t)=P{T≤t}=1−R(t)
-
失效密度函数f(t)
f(t)=dtdF(t)
-
失效率z(t)(风险函数)
指软件在t时刻尚未发生失效的条件下,在t时刻之后的Δt单位时间内(t,t+Δt)发生失效的概率,记作z(t)
z(t)=R(t)f(t)=−R(t)R′(t)R(t)=e−∫0tz(t)dt
-
失效强度λ(t)
指Δt单位时间内软件失效的概率。定义为当Δt→0时,软件在(t,t+Δt)上失效数的期望和Δt的比值。
例如在NHPP过程中,软件在t时刻发生的失效数为N(t),m(t)=E(N(t)),则失效强度λ(t)=dtdm(t)
注意:失效率是当软件在0~t时刻内没有发生失效的条件下,t时刻软件系统的失效强度
如果软件失效次数过程是泊松过程(HPP),则z(t)=λ(t)
-
平均无故障时间MTTF(Mean Time To Failure)
系统从开始正常工作到故障发生时所经历的时间间隔平均值。
-
平均故障间隔时间MTBF(Mean Time Between Failure)
系统发生相邻2次故障所经历的时间间隔平均值。
可以认为MTTF=MTBR=∫0∞tf(t)dt=∫0∞R(t)dt
-
平均故障修复时间MTTR(Mean Time to Repair)
系统发生故障到故障维修结束并且可以重新正常工作所经历时间间隔的平均值。
-
可用性A
任一随机时刻,软件处于可使用状态的能力。
A=f(R,M)=MTTF+MTTRMTTF
-
串并联模型可靠度计算
串联模型:
graph LR
1((begin)) --> 2((E1))
2((E1))--> 3((E2))
3((E2))--> 4(......)
4-->5((En))
5-->6((end))
Rs(t)=P{Xs>t}=P{min(X1,X2,...,Xn)>t}=P(X1>t,X2>t,...,Xn>t)=i=1∏nP(Xi>t)=i=1∏nRi(t)
并联模型:
graph LR
1((begin)) --> 2((E1))
1--> 3((E2))
1--> 4(......)
1--> 5((En))
2-->6((end))
3-->6
4-->6
5-->6
Rs(t)=P{Xs>t}=P{max(X1,X2,...,Xn)>t}=1−P{max(X1,X2,...,Xn)≤t}=1−P{X1<t,X2<t,...,Xn<t}=1−i=1∏n(1−Ri(t))
2.2软件可靠性建模思想、作用、影响因素
建模思想:根据软件可靠性相关测试数据,运用统计方法得出软件可靠性的预测值或估计值
作用:评估和验证
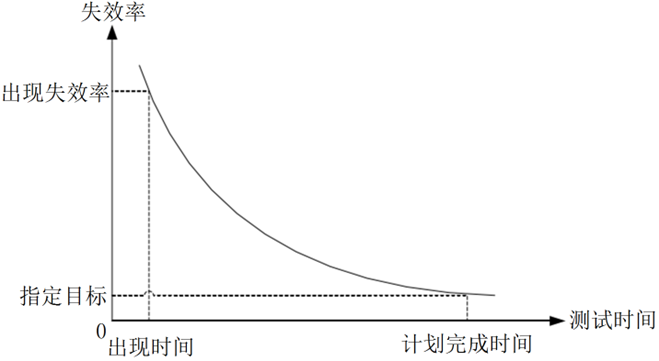
- 评估当前软件的可靠性水平
- 分析或预测要达到事先规定的软件可靠性水平,需要多少
影响因素:
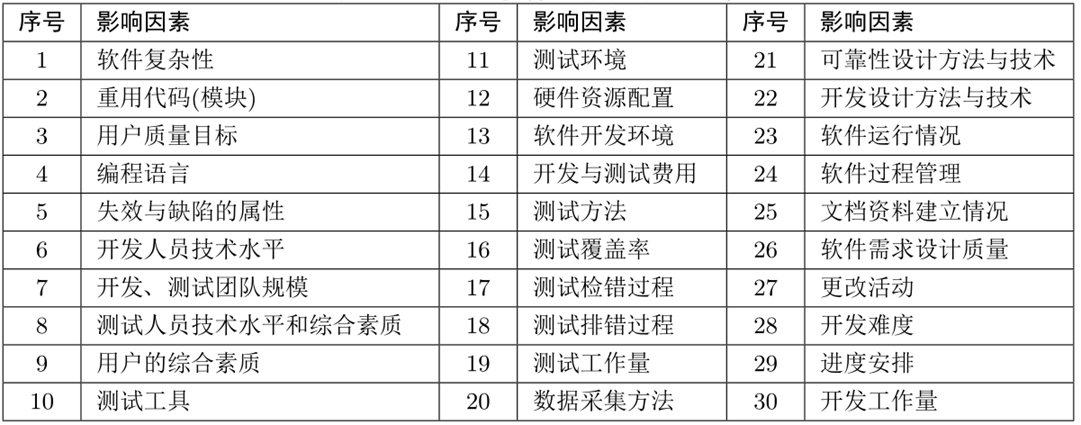
1-5为产品因素,6-14为项目因素,15-30为过程因素,以下为研究最多的因素:
-
测试覆盖率:常借助各种分布函数的形式来描述测试覆盖率,建立测试覆盖率和检测缺陷数的关系模型。
-
测试工作量:假设当前测试工作量所发现的平均缺陷数目与软件残留缺陷数目成某种比例关系,从而将测试工作量与软件失效率联系起来。
-
测试排错过程:一般假定排错过程中引入新错的概率与软件残存缺陷数成正比,提出改进可靠性模型。
-
测试检错过程:针对多种检错与排错方法可能给软件可靠性评估带来的影响,采用不同缺陷检测率函数
4.软件失效机理和故障传播分析
4.1软件失效机理分析
软件错误:软件错误是指在软件生存期内的不希望或不可接受的人为错误,其结果是导致软件缺陷的产生。
软件缺陷:软件缺陷是存在于软件(文档、数据、程序)之中的那些不希望或不可接受的偏差,如少一个逗号、多一语句等。其结果是软件运行于某一特定条件时出现软件故障,这时称软件缺陷被激活。
软件故障:软件故障是指软件运行过程中出现的一种不希望或不可接受的内部状态。
软件失效:软件失效是指软件运行时产生的一种不希望或不可接受的外部行为结果。泛指程序在运行中丧失了全部或部分功能、出现偏离预期的正常状态的事件,预期的正常状态应以用户的需求为依据。
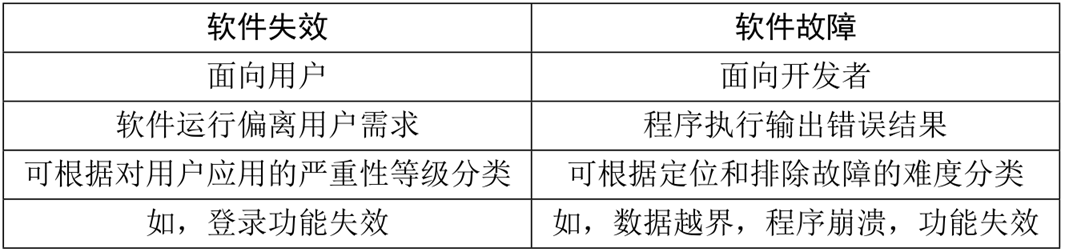
软件失效和软件故障的区别:
软件缺陷产生的原因:
-
软件及系统本身的复杂性不断增长,使得测试的范围和难度也随之增大;
-
与用户的沟通不畅使得无法及时获取最真实的用户需求;
-
需求不断变化,特别是敏捷开发模式下,测试开发和执行更难以跟上需求变化的步伐;
-
程序员编程错误,或植入多余功能;
-
进度压力导致测试被压缩,无法进行充分的测试;
-
对文档的轻视致使测试缺乏依据,带来测试的漏洞。
总的来说,是开发的软件与软件需求说明书、设计说明书的不一致,软件的实现未达到目标的用户潜在需求
4.2程序内部故障传播分析
软错误定义:由外部干扰(如宇宙射线或电磁干扰)或电荷翻转等原因导致的暂时性错误。软错误不涉及硬件的永久性损坏,通常通过刷新、重启或者数据重写可以解决。例子:单比特翻转。
-
动态指令跟踪
将程序转为动态指令序列。
-
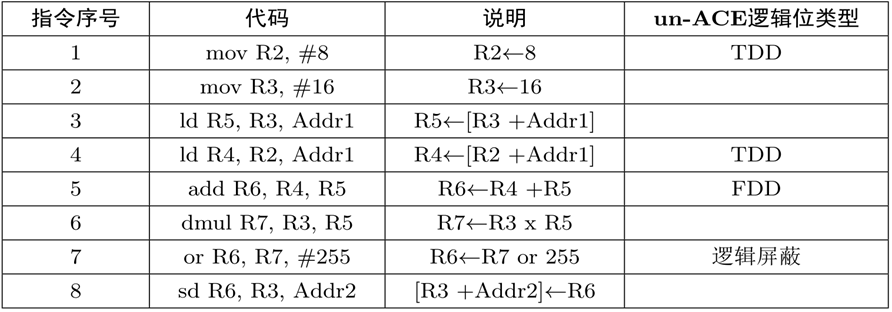
基于ACE分析的软错误分类
ACE逻辑位指影响程序运行结果的逻辑位,un-ACE逻辑位相反。
思想:以用户待分析的软错误作为输入,应用ACE分析将所有待分析的软错误划分为能影响结果、不能影响结果。un-ACE逻辑位分类:动态死指令和逻辑屏蔽。动态死指令分为直接动态死FDD和传播动态死TDD。
FDD指令:该指令的执行结果没有被其他指令所使用
TDD指令:该指令执行结果只被FDD或者TDD使用
逻辑屏蔽:有些位无论存储什么数据都不会对结果产生影响,如下图中R7的低八位被逻辑屏蔽。
-
基于DDG的软错误故障传播分析和崩溃预测
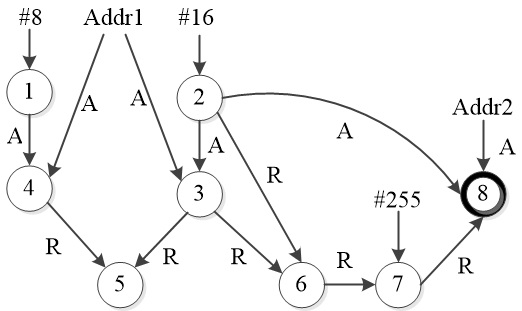
每条指令都产生新的节点,边上的A代表是作为有效地址参与运算,R代表作为寄存器数值参与运算,立即数则不需要标签。
-
故障传播分析和崩溃预测
给出软错误的位置和出现时间:(R,L,T)⇒(i,t),其中i表示软错误发生在DDG中第i个节点,t表示软错误(R,L,T)发生在节点t之后,t+1之前,因此该软错误只影响节点编号大于t的节点。
在DDG模型中从节点 i 开始搜索,寻找符合程序崩溃判断标准的节点。每访问一个新节点,意味着软错误传播到该节点并破坏相应的数据,需要判断该节点是否符合程序崩溃判断标准。如果符合,这个节点即为节点CrashNode(i,t);如果不符合程序崩溃判断标准,继续向后搜索,查看下一个节点。
程序崩溃判断标准:当一条包含污损地址的动态指令被执行时,重点关注以下地址:
-
函数调用开始前的目标地址
-
函数调用结束后的返回地址
-
分支程序的地址
-
访存指令中的内存地址或者IO地址
如果找不到CrashNode(i,t),说明是无提示数据错误,否则会引发程序崩溃。
4.3组件故障传播分析
-
组件间的软件失效传播
考虑体系结构的软件失效传播分析
串行系统:Pi,j表示从组件i转移到j的概率,组件Ci的失效概率为θi=1−Ri,EP(i,j)为i将失效传播给j的概率
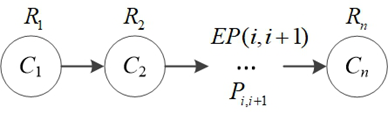


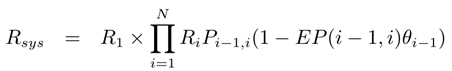
并行系统和分支系统都没讲怎么求Rsys
-
系统调用的组件失效传播(没讲,让自己看)
5.软件可靠性增长模型(1道)
有一道题,考查SRGM模型的基本原理(假设条件、可靠性模型的推导)
5.1经典SRGM模型
-
JM模型(很有可能)
模型假设:
- 软件中固有初始错误个数N0为一个未知常数;
- 软件中的各个错误是相互独立的,每个错误导致系统发生失效的可能性大致相同,各次失效时间间隔也是相互独立的;
- 测试过程中错误一旦被检测出即被完全排除,每次排错只排除一个错误,排错时间可以忽略不计,在排错过程中不引入新的错误;
- 软件的失效率在每个失效间隔时间内是常数,其数值正比于软件中残留的错误数,比例系数为ϕ;
- 软件的运行方式与预期的运行方式相似。
模型形式:
给定N0和ϕ的条件下,记Xi表示第i−1次故障时刻到第i次故障时刻间的时间,假定故障时间间隔X1,X2,...,Xn为相互独立的指数分布随机变量。由题意可知,第一个错误被排出后,失效率由N0变成了(N0−1)ϕ,以此类推z(xi)=ϕ[N0−(i−1)]
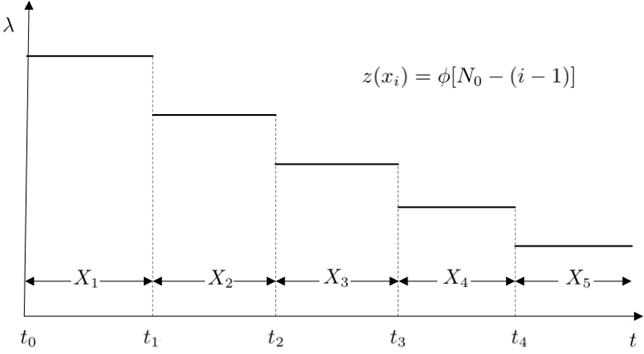
因此关于xi的概率密度为
f(xi)=z(xi)e−z(xi)xiF(xi)=1−e−z(xi)xiR(xi)=1−F(xi)=e−z(xi)xi=e−ϕ[N0−(i−1)]xiMTBF=E[Xi∣X1,X2,...,Xi−1]=∫0∞R(xi)dxi=ϕ[N0−(i−1)]1
-
NHPP类模型
NHPP类模型的基本假设:
(1)假设失效事件随机发生,测试人员和排错人员对失效的观察和故障的排除满足NHPP
(2)设{N(t),t≥0}为随机计数过程,N(t)为[0,t]内测试人员累计检测的故障数量,且E[N(t)]=m(t)为均值函数,满足m(0)=0
可以得到,
P[N(t)=k]=k!m(t)×e−m(t),k=0,1,2...m(t)=∫0tλ(t)dt
设t为上次失效的时间点,对于给定的时长x(x>0),软件可靠性(t,t+x]可以表示为:
R(x∣t)=P[N(t+x)−N(t)=0]=e−(m(t+x)−m(t))
GO模型
模型假设:
- 程序在同实际执行环境相差不大的条件下执行
- 在软件测试过程中,所有检测到的故障是相互独立的
- 测试未运行时的软件失效为0;当测试进行时,软件失效服从均值为m(t)的非齐次泊松过程(NHPP)
- t时刻累积检测到的故障数量m(t)变化率与当前剩余的故障数量a−m(t)成正比例,比例系数为b
- 每次只修正一个错误,当软件故障出现时,引发故障的错误被立即排除,并不会引入新的错误
模型形式:
设N(t)和m(t)分别表示区间[0,t]内的累计错误数和期望错误数,a为软件中的初始故障数,b为在t时刻每个错误的检出率,b>0,且有m(0)=0,m(+∞)=a。在[t,t+Δt]内期望的错误发生数与时刻t时期望的剩余错误数成比例,于是有
m(t+Δt)−m(t)=b(a−m(t))Δt
令Δt→0,则有
dtdm(t)=b×(a−m(t))
利用边界条件可得GO模型的均值函数表达式:
m(t)=a(1−e−bt),a>0,b>0
易知GO模型的失效强度函数为
λ(t)=dtdm(t)=abe−bt
考察随机变量序列{Xn,n=1,2,...},表示故障间的间隔时间,则Sn=∑k=1nXk(n=1,2,...表示第n个故障出现的时间,在给定Sn−1=s的条件下,Xn的条件可靠性函数(即软件可靠度)为
RXn∣Sn−1(t∣s)=P(Sn−Sn−1>t∣S1,S2,...,Sn−1)=exp{−[m(t+Sn−1)−m(Sn)]}=exp{−a[e−bs−e−b(t+s)]}
MO模型
模型假设:
- 当t=0,N(0)=0,即测试开始前,无失效发生
- 失效强度随着失效期望数的增加而呈指数递减,即λ(t)=λ0e−θm(t),其中为m(t)均值函数,θ>0是失效强度递减幅度参数,且λ0>0是初始失效强度
- 当Δt足够小,时间区间(t,t+Δt)内发生一次及以上失效的可能性为λ(t)Δt+o(t)
- 每个错误发生的机会相同,且严重等级相同,失效之间相互独立
- 软件的运行方式与预期的运行方式相似
模型形式:
由模型假设可知软件失效均值函数m(t)和失效强度函数λ(t)分别为:
m(t)=θ1ln(λ0θt+1)λ(t)=m′(t)=(λ0θt+1)λ0
定义ti为第i次失效发生的时间,x为从第i次失效开始前的执行时间,则软件失效i−1次后的可靠度函数为
R(x∣ti−1)=[λ0θ(x+ti−1)+1λ0θti−1+1]1/θ
ti−1时刻后的软件平均失效等待时间为
MTTFi=∫0∞R(x∣ti−1)dx=∫0∞[λ0θ(x+ti−1)+1λ0θti−1+1]1/θdx
Infletion S-shaped模型
模型假设:
- 程序在同实际执行环境相差不大的条件下执行。
- 部分故障在其他故障被发现之前不会被发现。
- 任何时间内故障的发现率与当前软件中残留故障成比例。
- 被隔离着的故障可以被完全修正。
- 故障检测率是一个不变常数。
模型形式:
b(t)为故障检测率函数,a(t)为软件总故障函数
dtdm(t)=b(t)(a(t)−m(t))
假设b(t)=b/(1+βe−bt),a为初始故障数
m(t)=1+βe−bta(1−ebt)λ(t)=(1+βe−bt)2ab(1+β)e−bt
6.数据驱动的软件可靠性模型
6.2基于时间序列的软件可靠性模型(二选一考)
ARIMA模型(模型形式+建模过程)
原始序列Yt,t=1,2,...,k,ARIMA(p,d,q)模型的一般形式为:
Xt=ϕ1Xt−1+ϕ2Xt−2+...+ϕpXt−p+ϵt−θ1ϵt−1−θ2ϵt−2−...−θqϵt−q,t∈Z
其中Xt是Yt通过d阶差分得到的数据,ϕi为自回归系数,q为移动平均阶数,θi为移动平均系数,ϵt独立同分布与均值为0,方差为σ2的白噪声过程。
- q=0,模型为AR(p)过程:
Xt=ϕ1Xt−1+ϕ2Xt−2+...+ϕpXt−p
- p=0,模型为MA(q)过程:
Xt=ϵt−θ1ϵt−1−θ2ϵt−2−...−θqϵt−q
- d=0,模型为ARMA(p,q)过程:
Xt=ϕ1Xt−1+ϕ2Xt−2+...+ϕpXt−p+ϵt−θ1ϵt−1−θ2ϵt−2−...−θqϵt−q,t∈Z
建模过程包括:平稳性检验、模型识别、参数估计/定阶、参数/模型检验
-
平稳性检验
一直差分直到通过游程检验。
-
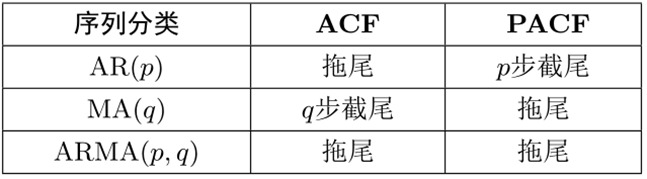
模型识别
计算ACF和PACF然后画图,进行识别。公式太复杂了不可能考…
-
参数估计/定阶
用最小二乘法求解得到参数ϕ1,...ϕp,θ1,...,θq,σ2
然后用AIC准则和SC准则进行判断,AIC和SC越小越好。
-
模型检验💩
白噪声检验,看不懂。
-
预测,然后根据差分次数还原为失效数据
GM(1,1)模型(难)
模型就是一个微分方程:
dtdX1+aX1=b
a,b为待定参数,X1是原始序列X0的一次累加值。
X1=[x1(1),x1(2),...,x1(n)]
令Z1是X1的紧邻均值生成序列:
Z1=[z1(2),z1(3),...z1(n)]
其中z1(k)=2x1(k)+x1(k−1),k=2,3,...,n
若a^=[a,b]T为待定参数列,记
Y=x0(2)x0(3)⋮x0(n),B=−z1(2)−z1(3)⋮−z1(n)11⋮1
由差分代替微分,可得GM(1,1)模型的最小二乘估计参数列满足:
a^=[a,b]T=(BTB)−1BTY
由以上条件可以得到时间响应函数的解为:
x1^(k+1)=(x0(1)−ab)e−ak+ab,k=1,2,...,n
又由x0^(k+1)=x1^k,可得
x0^(k+1)=(1−ea)(x0(1)−ab)e−ak,k=1,2,...,n
令k=1,2,...,n,由上式可得到GM(1,1)模型的预测值:
x0^=(x0^(1),x0^(2),...,x0^(n))
6.4软件可靠性组合模型
==EMD经验模态分解==
将原始数据f(t)分解为N个IMF分量和一个残差。
IMF分量:极值点和零点数目相等或相差一个;上包络线和下包络线关于时间轴对称
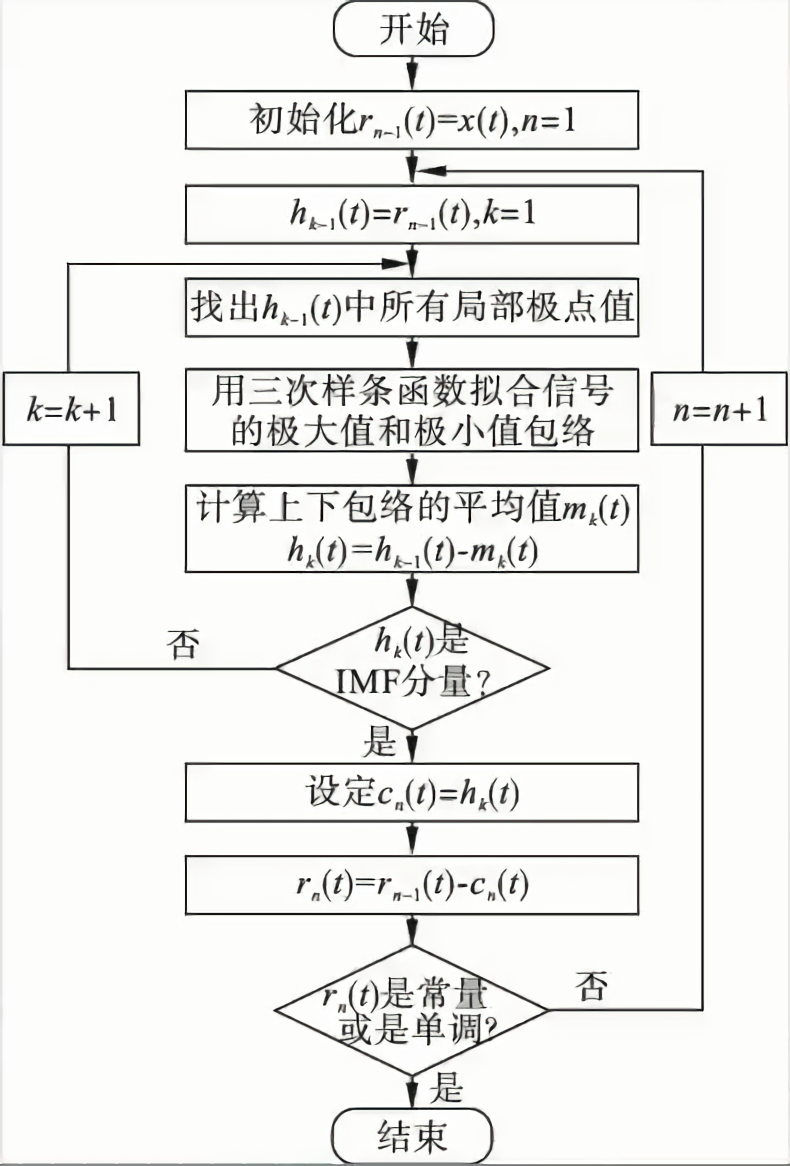
算法流程:
-
初始化:r0=x(t),i=1
-
求解第i个IMF:
初始化:h0(t)=ri−1(t),j=1
- 求出hj−1(t)的所有极值点
- 对极值点进行三次样条插值,得到上下包络线
- 计算上下包络线均值mj−1(t)
- hj(t)=hj−1(t)−mj−1(t)
- 判断hj(t)是否是IMF,是则imfi(t)=hj(t);否则j=j+1,转到开头。
-
ri(t)=ri−1(t)−imfi(t)
-
如果ri(t)极值点个数多于两个,则i=i+1,转到步骤2;否则分解完成。
流程图:
7.软件系统可靠性建模技术
7.1基于markov链的组件化系统可靠性分析
-
Cheung模型
组件化系统,已知每个组件的可靠性和用户剖面。基于假设:
- 组件之间的可靠度相互独立。
- 组件间的控制转移当作markov过程,下一个组件执行的概率只和当前组件有关。
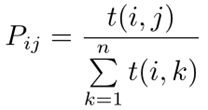
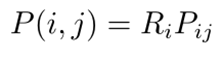

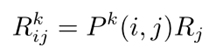
以下看不懂:
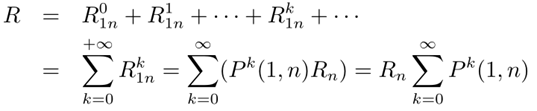
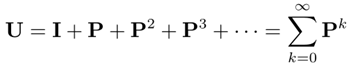

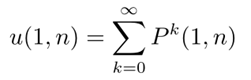
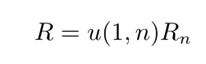
-
基于用户操作剖面
(定义)接口可靠性模型:POCi是组件Ci的服务接口集合,接口可靠性定义为r(p0),其中p0∈POCi,0≤r(p0)≤1
(定义)接口使用模型:POCi是组件Ci的服务接口集合,则满足∑p0∈POCim(p0)=1的全函数m就是Ci的一个接口使用模型。
(定义)概率迁移模型:g<Ci,Cj>表示组件从Ci迁移到Cj的概率
Ri=p0∈POCi∑r(P0)m(P0)
-
基于系统架构
串并联省略
并行结构:Rs=∏1≤j≤mRj
容错结构:RS=1−∏1≤j≤m(1−Rj)
调用返回结构:Rs=R1R2k,R1和R2分别是调用者和被调用者的可靠度。
7.2基于Petri网的体系结构软件可靠性分析
-
基于体系结构的Petri网SAPN
库所表示组件,变迁表示连接件。应该不考,课设要做。
-
基于(广义)随机Petri网
给定变迁的平均引发速率/实施速率λi,表示在可引发的情况下单位时间内平均引发次数。
1/λi表示变迁的平均引发延时/平均服务时间。一个变迁从可引发到引发需要时间,这段时间看作连续随机变量Xt,认为其服从指数分布Ft(x)=P{Xt≤x}=1−e−λtx,λt就是λi
同构MC:求出可达图后将实施速率换为λi即可。
-
Petri网化简
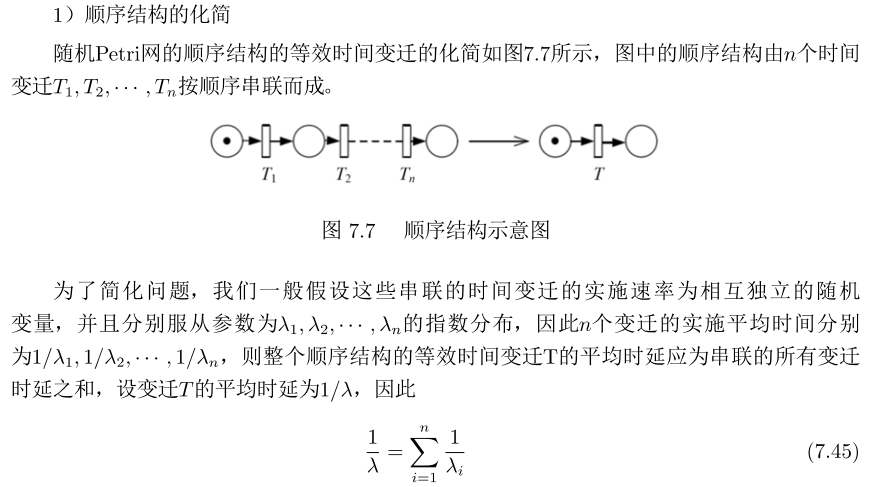
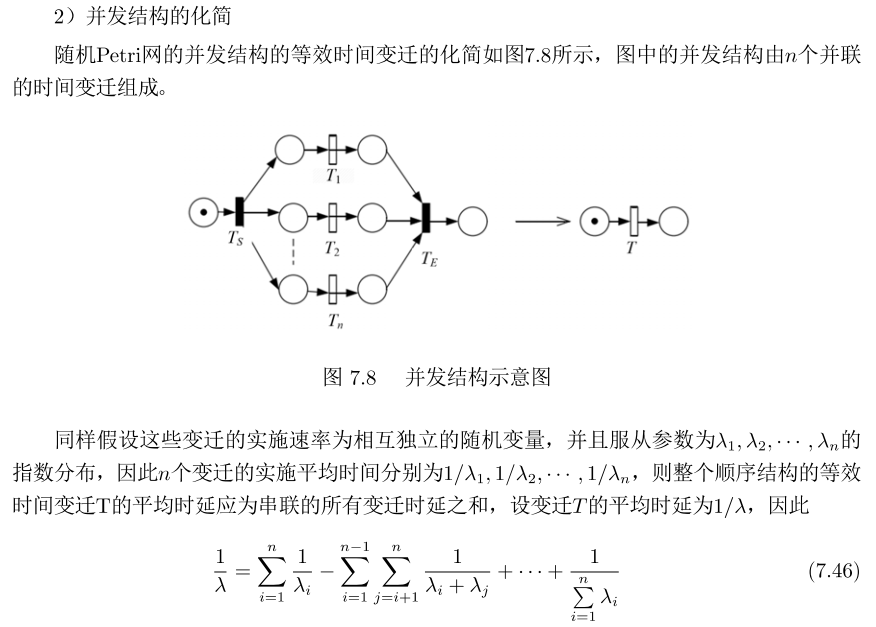
3)选择结构:
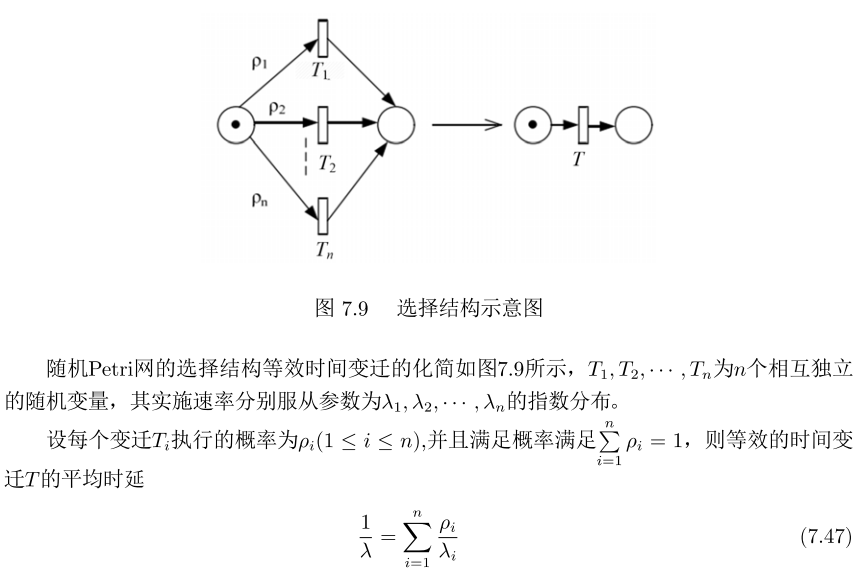
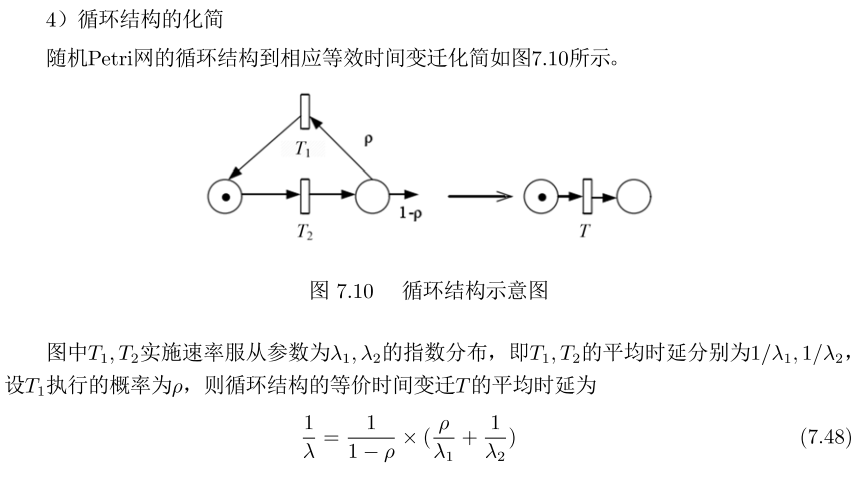
-
解题步骤
- 获取同构MC图,将变迁ti替换为引发速率λi
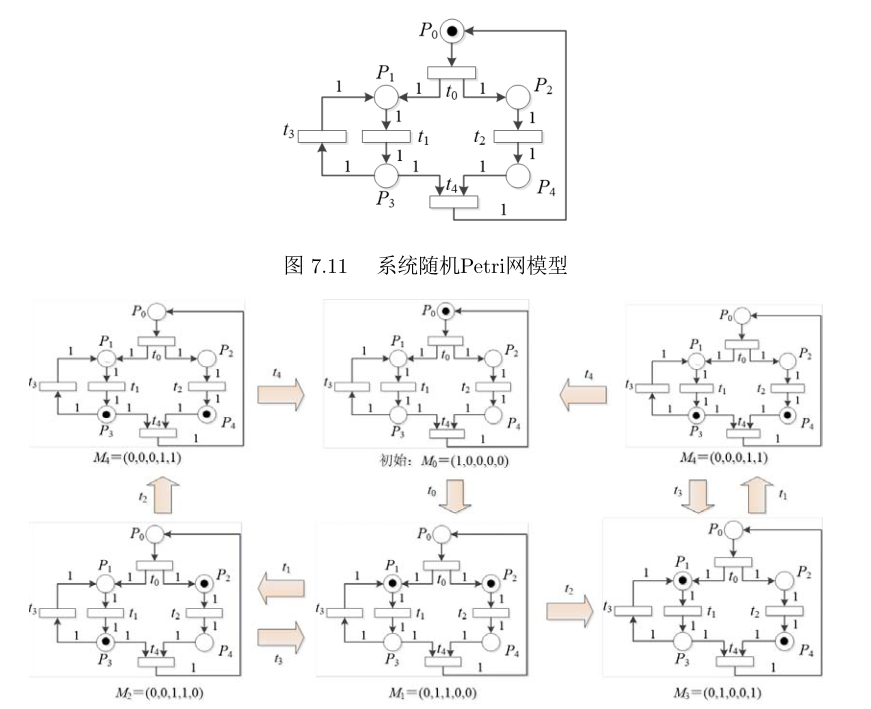
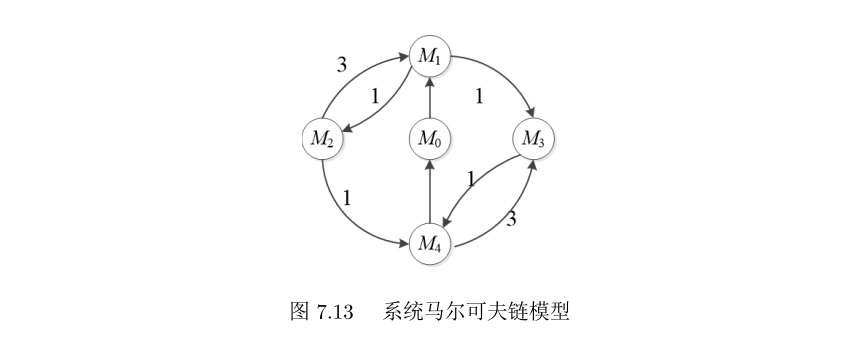
- 获取MC的状态转移概率矩阵A=[qij],qij的获取方式为:

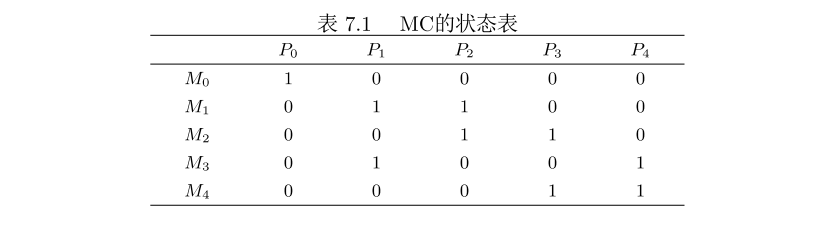
- 稳态概率分布π=(π1,π2,...,πn),通过以下方程求解π,得到可达标识的驻留概率P(Mi)
π×A=0i=1∑n=1
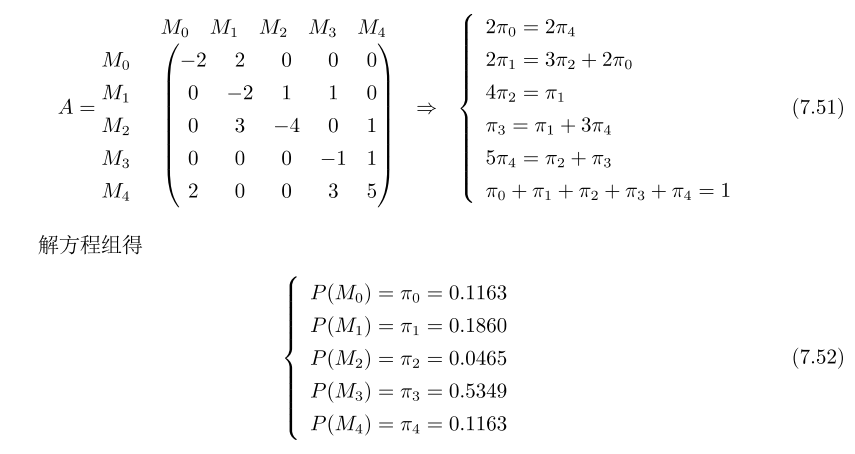
-
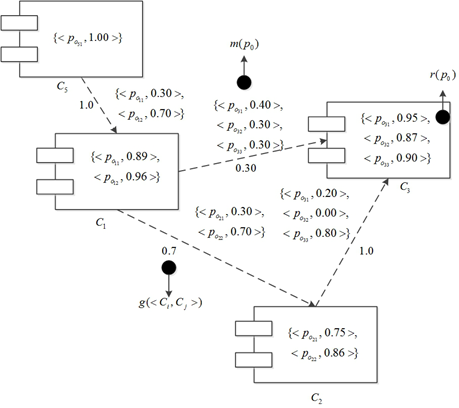
可达标识Mi驻留时间:
对于矩阵A,对角线元素qii表示可达标识Mi驻留速率,因此可达标识Mi驻留时间为:
τ1=1/2=0.5τ2=0.5τ3=1/4=0.25τ1=1/1=1τ1=1/5=0.2
每个库所Pi出现的概率:
P(M(P0)=0)=P(M1)+P(M2)+P(M3)+P(M4)=0.8837,P(M(P0)=1)=1−0.8837......
变迁在每个标识的引发概率:
P(M[ti>)=∑i∈出边λiλi

每个变迁的使用概率:

8.软件系统可靠性分析技术
8.1故障树分析
-
故障树简化
-
求最小割集/最小径集
-
计算顶事件发生概率
与事件用串联公式,或事件用并联公式
-
计算底事件的结构重要度、概率重要度、关键重要度
假设T=X1+X2X3
结构重要度:反应底事件在结构中的重要性。
如果一共有n个底事件,先求出nϕ(i),Iϕ(i)=2n−1nϕ(i)
求nϕ(i)就是看Xi从1变到0,剩下的底事件不变,最终顶事件也从1变到0,这种情况次数之和。
概率重要度:组件不可靠度变化引起系统不可靠度变化的程度。
Δgi(t)=∂Fi(t)∂Fs(t)
此例中Fs(t)=1−(1−F1(t))(1−F2(t)F3(t))
因此Δg1(100)=1−F2(100)F3(100)=0.953,其余略。
关键重要度:第i个组件故障率变化引起系统故障概率的变化率
IiCR(t)=Fs(t)Fi(t)Δgi(t)
根据概率重要度的计算公式,可以求出Fs(t),F1(t)等值。
9.软件系统可靠性设计方法
9.1避错设计
结合你的实际开发过程,谈谈七大原理:
- 简单原理(Simplicity Principle)
核心思想: 对需求全面细致分析、抽象与逐步求精、模块化与信息隐藏
实际开发中的应用:
- 代码简洁清晰:在开发过程中,保持代码简洁,不使用冗余的库或功能。例如,只使用必要的设计模式,不盲目使用工厂模式或单例模式。
- 功能单一:每个模块、类、函数只承担单一职责(SRP原则),这样可以减少因模块间耦合引起的错误。
- KISS原则:保持简单(Keep It Simple, Stupid)。比如在数据处理时,尽量选择简单的逻辑处理,而不是使用复杂的嵌套循环。
示例: 在输入校验中,使用正则表达式可以有效简化代码逻辑。相比于嵌套多层的if-else判断结构,正则表达式提供了简洁而高效的输入校验。
- 同型原理(Consistency Principle)
核心思想: 结构形式统一、定义与说明统一、编程风格统一,以统一达到软件的一致性、规范化
实际开发中的应用:
- 统一命名规范:变量、函数、类命名风格保持一致,避免混用不同的命名规则(如驼峰命名与下划线命名)。
- 一致的错误处理方式:统一使用异常(Exception)处理错误,而不是在有的地方用返回值来判断,有的地方用异常捕获。
- 统一的UI/UX设计:前端页面中的交互方式和视觉风格保持一致,避免用户因不一致的操作引入错误。
示例: 在API开发中,所有API响应都采用一致的结构,如:
1
2
3
4
5
| {
"code": 200,
"message": "Success",
"data": {...}
}
|
这种一致性设计可以让前端处理API响应时无需区分不同结构,减少错误。
- 对称原理(Symmetry Principle)
核心思想: 大至整个系统的软件结构,小至程序中的逻辑控制、条件、状态和结果等的处理形式力求对称
实际开发中的应用:
- 请求-响应对称:RESTful API设计时,请求结构和响应结构应保持对称。例如,POST请求传递的数据结构应该与GET请求获取的数据结构类似。
- 输入输出对称:函数输入和输出应该保持一致,函数执行过程中如果有异常情况,应该返回标准错误类型,而不是返回不一致的数据结构。
示例: 用户输入和结果输出使用同一格式,如输入JSON结构,返回也使用JSON结构,而不是混用XML或HTML。
- 层次原理(Hierarchical Principle)
核心思想: 通过将系统划分为不同的层次或模块,使得每个层次的功能独立且责任明确,从而减少错误的传播和影响。
实际开发中的应用:
- 分层架构:如MVC架构,将前端视图、业务逻辑、数据库访问分离开,确保修改一层时,不会影响其他层。
- 模块化设计:将功能拆分为独立模块,比如在微服务架构中,每个微服务负责单一功能,减少耦合。
示例: 在大型Web应用中,划分为Controller层、Service层、DAO层。Controller负责接收请求,Service处理业务逻辑,DAO层负责数据库操作,这样错误发生时能够快速定位到具体层次。
- 线型原理(Linearity Principle)
核心思想: 避免复杂的分支和循环,保持程序的线性结构,降低错误率。
实际开发中的应用:
- 减少分支判断:尽量减少if-else判断,使用策略模式或状态模式替代复杂的判断。
- 避免深度嵌套:使用早返回(early return)和guard clauses,减少代码的嵌套层级,保持代码的直线流动性。
示例:
1
2
3
4
5
6
7
8
|
def process_data(data):
if data is None:
return "Error: No data"
if not data.is_valid():
return "Error: Invalid data"
return "Success"
|
- 易证原理(Ease of Verification Principle)
核心思想: 是保持程序在逻辑上容易证明的原理
实际开发中的应用:
- 静态分析工具:使用代码静态分析工具(如SonarQube)来检测代码中的潜在问题。
- 健壮性及安全设计原理(Robustness and Security Design Principle)
核心思想: 软件健壮性是一种非功能性的需求,是指在软件的运行过程中,不管遇到什么挫折情况,力求软件能完成所赋予功能的能力
实际开发中的应用:
- 异常处理:捕获可能发生的异常并进行处理,避免因异常未处理导致系统崩溃。
- 输入校验:对用户输入进行严格校验,防止SQL注入、XSS攻击等安全问题。
- 超时和重试机制:对于外部请求,设置超时和重试机制,防止长时间阻塞或失败。
示例: 使用try-except结构来捕获异常,防止程序崩溃:
1
2
3
4
| try:
result = 10 / user_input
except ZeroDivisionError:
result = None
|
同时,使用输入校验防止恶意输入:
1
2
| if not isinstance(user_input, int) or user_input < 0:
raise ValueError("Invalid input")
|
9.2查错设计
**被动差错:**在软件中插入检错程序,定期定点对软件运行中的输入数据、操作指令、关键信息(数值)和系统的各种状态进行合理性、逻辑性检查和再确认,目的是及时发现错误和确定出错部位。
**主动差错:**通过错误检测程序主动地对系统进行搜索,并指示所搜索到的错误。
区别:被动差错只有当错误传递到该接收判断时才能进行判断,而主动差错不一样。
9.3纠错设计
只能减少软件错误造成的危害,如故障隔离技术等
9.4容错设计
查错设计是指在设计中赋予程序某些特殊的功能,使程序在运行中自动查找存在错误的一种设计方法。
结构容错(如:N-版本程序)、信息容错(如:奇偶校验、CRC校验等)、时间容错(如:指令重复执行和程序卷回)等
时间容错:
- 指令重复执行:检测到错误重复执行n次
- 程序卷回:出现错误回到事先设置的恢复点重试,瞬时故障可以恢复正常。
10.软件系统可靠性测试与验证
软件可靠性测试和功能测试区别:
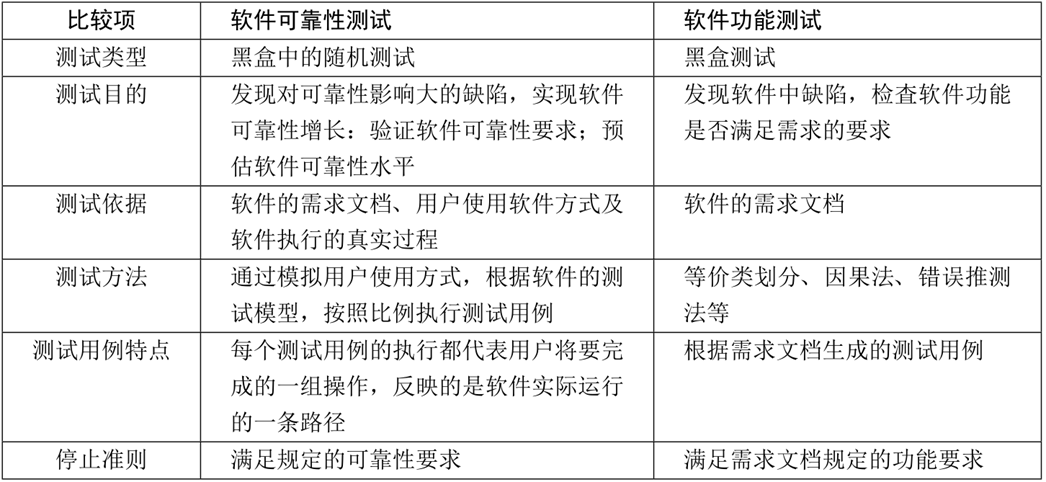
软件可靠性测试类型:
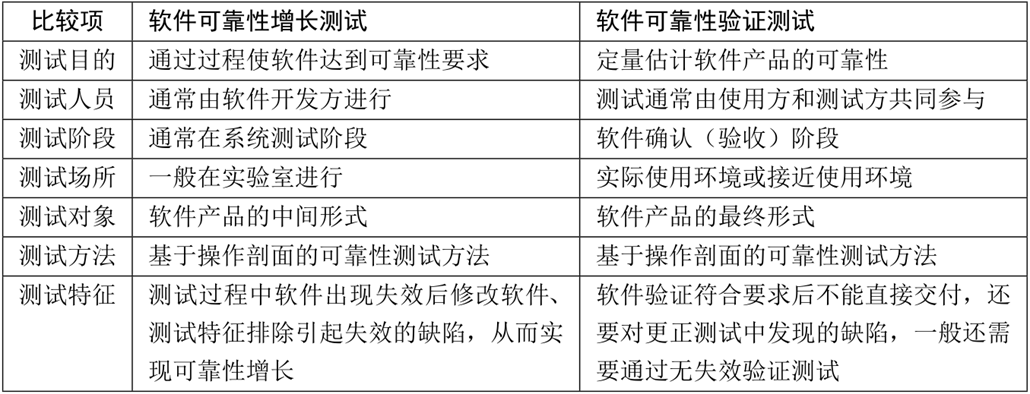
10.1基于操作剖面的可靠性测试方法
掌握如何生成测试用例:
给定操作剖面{(O1,P(O1)),(O2,P(O2)),...,(On,P(On))},利用累积分布函数F(Oi)=∑j≤iP(Oi),生成概率向量[0,F(O1)],(F(O1),F(O2)],...,(F(On),1)]。然后用均匀分布采样r—U(0,1),判断r在哪个区间从而得到下一个操作为Oi。
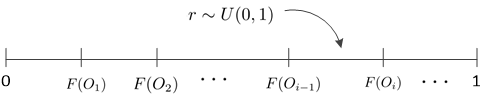
10.2基于使用模型的可靠性测试方法
掌握如何生成测试用例:
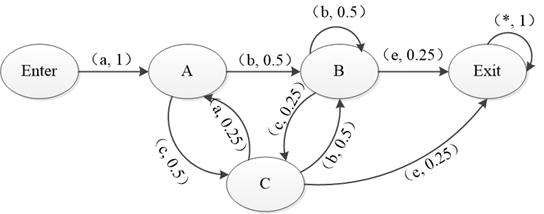


11.软件系统可靠性工程(1道)
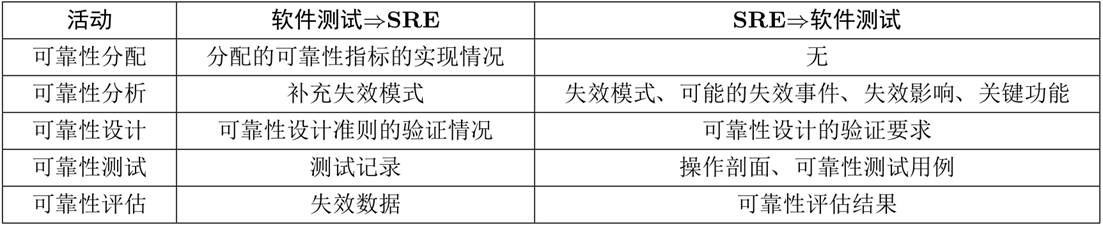
11.1软件可靠性工程的活动分析
各个阶段的交互
系统定义阶段:
进行系统级别的可靠性指标分配、可靠性要求等
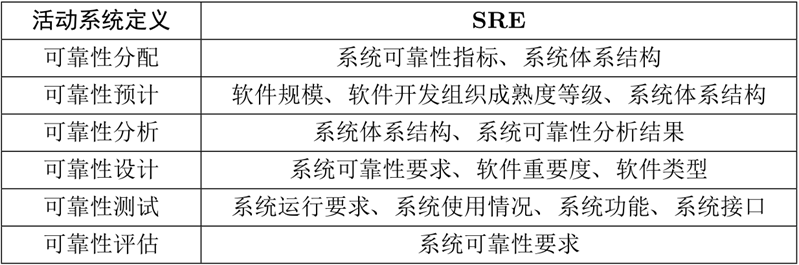
需求分析阶段:
需求分析提供相似软件的历史信息、可靠性需求等,可靠性工程提供操作剖面、软件故障模式、失效影响等
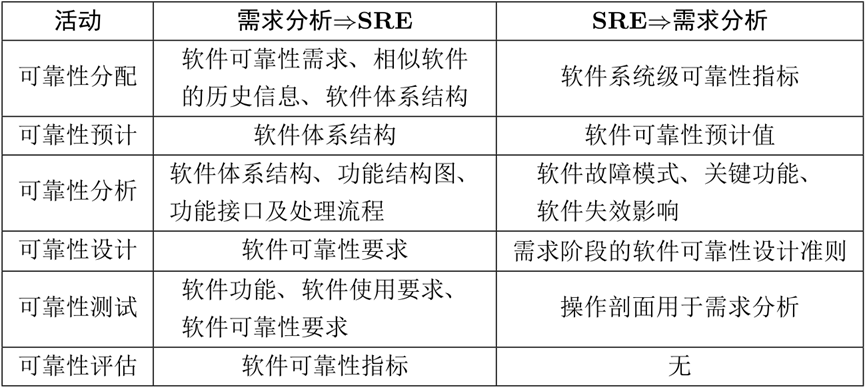
设计阶段:
从软件模块、组件的层面,设计阶段提供了模块的复杂度和关键度,分析了组件间调用关系等
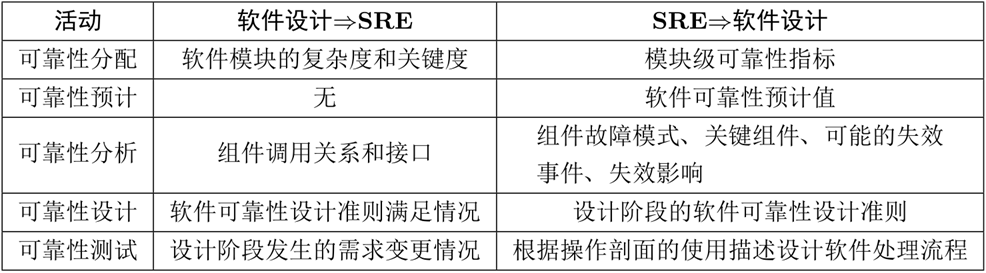
编码阶段:
提供了代码复杂度用于可靠性分配,模块调用关系用于可靠度分析,提供可靠性设计准则的满足情况
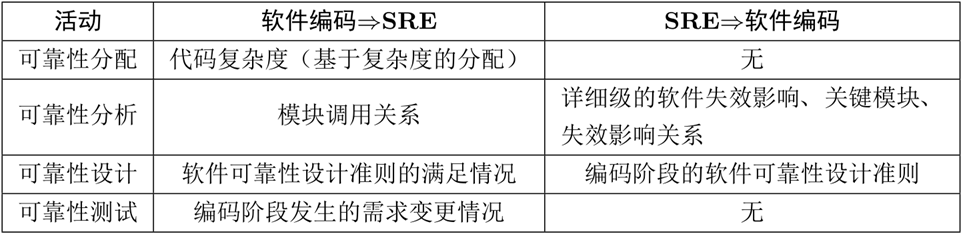
测试阶段:
提供分配的可靠性指标的实现情况、可靠性设计准则的验证情况、测试记录、失效数据。
SRE为软件测试提供了可能的失效模式、失效事件,返回了可靠性评估结果