计算机系统基础(一)笔记——Week3 运算电路基础

Week3 运算电路基础

3.2 从C表达式到逻辑电路

• 基本数据和运算

基本数据类型：有/无符号整数、浮点数、位串

基本运算符号：算数、位、逻辑、移位、拓展和截断

• 表达式都会转换为指令

例：y=(x>>z)+k的指令序列：

sarw $2, %ax ; x>>2
addw %bx,%ax ; (x>>2)+k

对于第一条：将操作数2和R[ax]送移位器中运算

对于第二条：将R[ax]和R[bx]送整数加减器中运算

• 指令集中涉及到的运算

  1. 定点数：
     • 算术运算：
       • 带符号整数：取负、符号拓展、加减乘除、算术移位
       • 无符号整数：0拓展、加减乘除、逻辑左移、逻辑右移
     • 逻辑运算：与或非
  2. 浮点数：加减乘除

  指令集的运算操作都在运算电路中进行。

3.3 C语言程序中的各类运算

• 算术运算

• 按位运算

  主要对位串实现掩码操作和对应处理（多媒体数据或状态/控制信息）

  例：从y中提取低位字节，使高位字节为0？

  &操作，如y & 00FF

• 移位运算

  用来扩大或缩小2、4、8…倍

  由x类型区分逻辑移位（unsigned）和算术移位

  判断溢出：

  1. 逻辑移位（补0）：移出的高位为1→溢出
  2. 算术移位（右移时高位补符）：移出的位不等于新的符号位→溢出

  例：对于n位(n≥8)的变量x，要求实现如下功能

  • x的最高有效字节不变，其余全为0

    (x>>(n-8))<<(n-8)

  • x的最低有效字节不变，其余全为0

    x & 0xFF

  • x的最低有效字节全变0，其余各位取反

    ((x ^ ~0xFF) >> 8)<<8

  • x的最低有效字节全变1，其余不变

    x | 0xFF

• 逻辑运算

• 拓展、截断运算

  拓展：短转长

  无符号0拓展、带符号符号拓展

  截断：长转短

  例：

  int i=32768
  short si=(short) i;
  int j=si;
  /*
  i≠j
  i=32768 → 00008000
  si=-32768 → 8000
  j=-32768 → FFFF8000
  */

3.4 整数加减运算

• 指针、地址等通常被说明为无符号整数，因此进行指针或地址运算时，需要进行无符号整数的加减运算
• 无符号整数和带符号整数的加减运算电路完全一致，这个运算电路称为整数加减运算部件，基于带标志加法器实现
• 计算机中的加法器，只有n位，所以是模$2^n$运算系统

n位带标志加法器

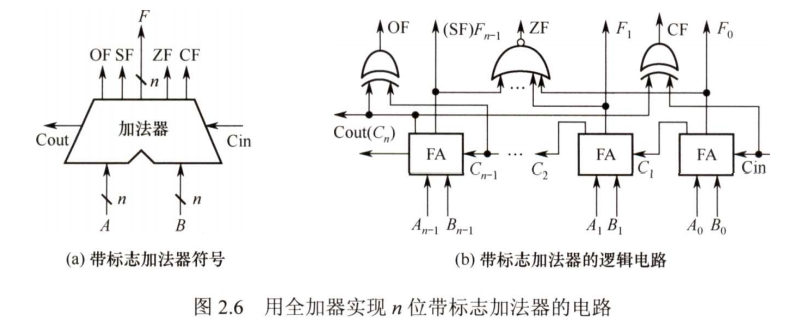
n位无符号数加法器无法用于两个n位带符号整数（补码）相加，无法判断溢出，因此采用带标志加法器

• $OF=C_n\oplus C_{n-1}$
• $SF=F_{n-1}$
• $ZF=1$仅当$F=0$
• $CF=C_{out}\oplus C_{in}$，即$C_{in}=0$时，$CF$为进位$C_{out}$；$C_{in}=1$时，$CF$为进位$C_{out}$取反

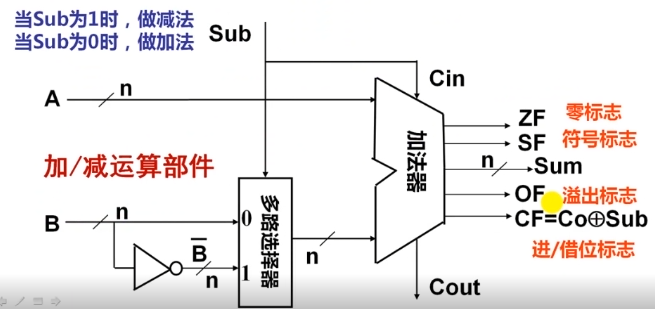
整数加/减运算部件

• 补码加减运算公式

  $[A+B]_{补}=[A]_{补}+[B]_{补}（MOD\ 2^n）$

  $[A-B]_{补}=[A]_{补}+[-B]_{补}（MOD\ 2^n）$

  注意符号位（最高有效位MSB）和数值位一起参与运算

  

  注意：

  • 计算机中所有运算基于加法器
  • $[-B]_{补}=[B]_{反}+1$
  • 加法器不判定对错，总是取低n位，并生成标志信息

  为什么要生成标志信息，保存条件标志？

  因为在条件转移指令中被用作是否转移执行的条件

  如何得到标志位？

  OF：如果A和$[B]_{反}$同号但与sum不同号，1；否则0

  SF：sum的符号

  ZF：sum=0则为1；否则0

  CF：$Cout\oplus Sub$

整数加法举例

做加法时，主要判断是否溢出

==无符号加溢出条件：CF=1==

==带符号加溢出条件：OF=1==

若n=8，计算107+46=0110 1011+0010 1110=0 1001 1001

无符号：sum=153，CF=0无溢出

带符号：sum=-153，OF=1溢出

整数减法举例

1001+1010= (1) 0011

OF=1、ZF=0、SF=0、借位CF=0

带符号：-7-6=3，显然不对，发生了溢出

无符号：9-6=3，没发生溢出

1101+1011= (1) 1000，OF=1溢出

OF=0、ZF=0、SF=1、借位CF=0

带符号：-3-5=-8，没发生溢出

无符号：13-5=8，没发生溢出

==无符号减溢出条件：差为负数，即CF=1；==

==带符号减溢出条件：和带符号加一致，OF=1==

做减法比较两个数大小：

假设是A-B

无符号：CF=0，A>B

9>6，因此CF=0

13>5，因此CF=0

有符号：OF=SF，A>B

-7<6，因此OF≠SF

-3<5，因此OF≠SF

如何用程序判断是否溢出？

• 无符号整数加法判断溢出

bool uadd_ok(unsigned x,unsigned y)
{
    unsigned sum=x+y;
    return sum>=x;
}

发生溢出则$sum=x+y-2^n$，一定有sum<x and sum<y

• 带符号整数加法判断溢出

$$sum=\left\{ \begin{aligned} &x+y-2^n (2^{n-1}\le x+y)\ 正溢出\\ &x+y (-2^{n-1}\le x+y <2^{n-1})\\ &x+y+2^n(x+y<-2^{n-1})\ 负溢出\\ \end{aligned} \right.$$

bool tadd_ok(int x, int y) {
    int sum = x+y;
    int neg_over = x < 0 && y < 0 && sum >= 0;
    int pos_over = x >= 0 && y >= 0 && sum < 0;
    return !neg_over && !pos_over;
}

• 带符号整数减法判断溢出

int tsub_ok(int x, int y) {
	return tadd_ok(x, -y);
}

注意：该程序有bug!!!

当x=0,y=0x8000 0000时，函数判断错误

因为此时$x=0,y=-2^{31},x-y=2^{31}$，发生正溢出

而调用程序时，由于-y还是8000 0000，小于0，不满足溢出条件