离散数学笔记-近世代数

第六章-典型的代数系统

6.1 群

6.1.1 半群和独异点

定义

• 对于代数系统$V=<S,\cdot>$，若$\cdot$可结合，则$V$为半群。
  进一步，若半群$V$具有单位元，则称$V$为独异点。
• 典型的半群有$<Z^{+},+>,<N,+>,<Z,+>,<Q,+>,<R,+>$等。

6.1.2 群

定义

• 对于代数系统$<G,\cdot>$，若$\cdot$可结合，存在单位元$e\in G$，且对于$G$中的任意元素$x$都有$x^{-1}\in G$，则称$G$为群。
  • 典型的群有$<Z,+>,<Q,+>,<R,+>,<Z_{n},\oplus>$
• 有限群：群$G$为有穷集，如$<Z_6,\oplus>$，其中$|G|$称为群的阶
  无限群：群$G$为无穷集，如$<Z,+>,<Q,+>,<R,+>$是无限群
  平凡群：只含单位元的群，如$<\lbrace0\rbrace,+>,<\lbrace1\rbrace,\times>$
  交换群/Abel群：群中的二元运算可交换

一些性质

• $\forall x\in G,x^{n}$定义如下：
  • $x^{0}=e$
  • $x^{n+1}=x^{n}x,n\in N$
  • $x^{-n}=(x^{-1})^{n}$
• $G$中幂运算满足：
  • $\forall a \in G,(a^{-1})^{-1}=a$
  • $\forall a,b \in G,(ab)^{-1}=b^{-1}a^{-1}$
  • $\forall a \in G,a^{n}a^{m}=a^{n+m}$
  • $\forall a \in G,(a^{n})^{m}=a^{nm}$
• $\forall a,b \in G$，方程$ax=b$和$ya=b$在$G$中有解，且唯一
  $prove:$
  • 存在性：$a(a^{-1}b)=(aa^{-1})b=eb=b$
  • 唯一性：若$c$是方程的解，则$c=(aa^{-1})c=a^{-1}(ac)=a^{-1}b$
• $G$为群，则$G$满足消去律，即$\forall a,b,c\in G$,有

  $$ab=ac \Rightarrow b=c \\ ba=ca \Rightarrow b=c$$

特殊的群

• $Klein$四元群

$$\def\arraystretch{1.25} \begin{array}{c|c c} \cdot & e & a & b & c \cr\hline e & e & a & b & c\cr a & a & e & c & b\cr b & b & c & e & a\cr c & c & b & a & e \end{array}$$

• 单位元$e$
• 每一个元素的逆元都是自身
• $a,b,c$中任意2个元素运算$\cdot$结果是另外一个
• 群中元素的阶：$|e|=1,|a|=|b|=|c|=2$

6.1.3 群中元素的阶

定义

• $x\in G$，使得$x^{k}=e$成立的最小正整数$k$称为$x$的阶，记作$|x|=k$，此时$x$称为$k$阶元。若不存在这样的$k$，则$x$称为无限阶元
  • $<Z,+>$中，$|0|=1$
  • $<Z_{6},\oplus>$中，$|0|=1,|1|=|5|=6,|2|=|4|=3,|3|=2$
  • $<Z_{8},\oplus>$中，阶为4的元素有2、6，$|4|=2$

q：如果$G$是有限群，那么$G$包括无限阶元吗？
a：若$G$为有限群，$\forall a\in G$为无限阶元，则

$$\lbrace a^{-\infty}...a^{-1},a^{0},a^{1},a^{2}...a^{\infty}\rbrace \subset G$$

且$a^{-\infty}\not = ... \not = a^{-1} \not = a^{0} \not = a^{1} \not = a^{2} \not = ...\not = a^{\infty}$
(若$\exists n,m\in Z$，且$n\not = m$，有$a^{n}=a^{m}\Rightarrow a^{|n-m|}=e$，与已知矛盾)
即，无限阶元会产生无穷个元素，显然$G$不可能是有限群

一些性质

• 设$G$为群，$a\in G$，且$|a|=r$，则
  • $a^{k}=e$的充分必要条件为 $r|k$
    必要性：已知$a^{k}=e$，由除法得$k=pr+q(0\le q \le r-1,p\in Z)$，从而

    $$a^q=ea^{q}=(a^r)^{p}a^{q}=a^{k}=e$$

    因此$q=0$
  • $|a|=|a^{-1}|$
    $|a^{-1}|=t$，则$(a^{-1})^{r}=(a^r)^{-1}=e$，则$t|r$
    同理可证$r|t$，因此$t=r$
  • $r\le|G|$
    已知$|a|=r$，则

    $$a^{0} \not = a^{1} \not = a^{2}\not = ...\not = a^{r-1} \\ a^{r}=a^{0},a^{r+1}=a^{1},...,a^{2r-1}=a^{r-1} \\ a^{-1}=a^{r-1},a^{-2}=a^{r-2},...,a^{-r}=a^{0}$$

    且$\lbrace a^{0},...,a^{r-1}\rbrace\subset G$,即$r\le|G|$

6.1.4 子群

定义

• 设$<G,\cdot>$是群，$H$是$G$的非空子集，如果$H$关于$G$中运算$\cdot$构成群，则称$H$是$G$的子群，记作$H\le G$
  若$H$是$G$的子群，且$H\sub G$，则称$H$是$G$的真子群，记作$H<G$
  $G$和$\lbrace e\rbrace$都是$G$的子群，称为$G$的平凡子群
• eg：$nZ(n\in N)\le <Z,+>$，且当$n\not =1$时，$nZ<Z$

子群的判定定理

下面给出判断子群的三条定理：

• 定理一：设$<G,\cdot>$是群，$H$是$G$的非空子集，$H\le G$当且仅当：
  • $(1)\forall a,b \in H$，有$a\cdot b\in H$
  • $(2)\forall a \in H$，有$a^{-1}\in H$
• 定理二(子群判定定理)：设$G$为群，$H$是$G$的非空子集，$H\le G$当且仅当 $\forall a,b\in H$有$a\cdot b^{-1}\in H$

充分性：
已知$H\le G$，则$\forall a,b \in H$，有$a\cdot b\in H 且b^{-1} \in H \Rightarrow a\cdot b^{-1}\in H$
必要性：
由$\forall a,b\in H有a\cdot b^{-1}\in H$
$1.$令$b=a$，则$a\cdot a^{-1}=e\in H$，即$H$中单位元存在
$2.$令$a=e$，则$e\cdot b^{-1}=b^{-1}\in H$，即$H$中元素均有逆元
$3.\forall a,b \in H$，则$b^{-1}\in H$，则$a\cdot (b^{-1})^{-1} \in H \Rightarrow a\cdot b \in H$，即$H$对$\cdot$运算封闭

• 定理三(有限群的子群判定定理)：设$G$为群，$H$是$G$的非空子集。如果$H$是有穷集，则$H$是$G$的子群当且仅当$\forall a,b \in H$，有$a\cdot b\in H$

充分性易证，下证必要性
$1.$由于$\forall a,b \in H$，有$a\cdot b\in H$，即$H$对$\cdot$运算封闭
$2.$由于$H$是有穷集，故$\forall a\in H$，有$|a|=r\Rightarrow a^{r}=e\in H$，即$H$中存在单位元
$3.$由$a^{r-1}\cdot a=e \Rightarrow a^{-1}=a^{r-1}$，即$H$中任意元素均有逆元

特殊子群

• 循环群：设$G$为群，$a\in G$，令$H=\lbrace a^{k}|k\in Z\rbrace$，则$H$是$G$的子群，称为由$a$生成的子群，记作$<a>$，称为循环群
  • 整数加群$<Z,+>$，由$2$生成的子群是$<2>=\lbrace 2k|k\in Z \rbrace=2Z$
  • 模6加群$<Z_{6},\oplus>$中，$<2>=\lbrace 0,2,4 \rbrace$
• 设$G$为群，令$C$为$G$中所有可交换的元素构成的集合，即$C=\lbrace a|a\in G \land \forall x \in G(ax=xa)\rbrace$，则$C$是$G$的子群，$C$称为$G$的中心
  • 对于$Abel$群$G$，$G$的中心就是其自身
  • 如果中心是$\lbrace e \rbrace$，则$G$是无中心的

$1.$设$a,b\in C$，则$a\in G,b\in G \Rightarrow b^{-1} \in G$，且对$\forall x \in G$，有$ax=xa$

$$bx=xb\Rightarrow x=b^{-1}xb \Rightarrow xb^{-1}=b^{-1}x$$

因此$b^{-1}\in C$，故$ab^{-1}x=axb^{-1}=xab^{-1}$

• 共轭子群：设$H\le G,x\in G$，证明：$xHx^{-1}=\lbrace xhx^{-1}|h\in H\rbrace$是$G$的子群，称为$H$的共轭子群

$1.$设$xax^{-1},xbx^{-1}\in xHx^{-1}$，则$a\in H,b\in H,b^{-1}\in H\Rightarrow ab^{-1}\in H$
$2.$$xax^{-1}(xbx^{-1})^{-1}=xax^{-1}xb^{-1}x^{-1}=xab^{-1}x^{-1}\in xHx^{-1}$，由子群判定定理，原式得证

• 例：设$G$是群，$H,K$是G的子群，证明
  （1）$H\cap K$也是$G$的子群

$\forall a,b\in H\cap K$，则$a\in H 且 a\in K,b^{-1}\in H 且 b^{-1}\in K$，由于$H\le G且K\le G$，因此$ab^{-1}\in H且ab^{-1}\in K$，因此$ab^{-1} \in H\cap K\Rightarrow H\cap K\le G$

（2）$H\cup K\le G\iff H\sube K \vee K\sube H$

充分性$\Leftarrow$显然成立
下证必要性$\Rightarrow$：假设$H\not \sube K\wedge K\not \sube H$，则$\exists h\in H \wedge h \notin K,\exists k\in K \wedge k \notin H$，则$hk\notin H$（否则$k=h^{-1}(hk)\in H$，矛盾）,同理$hk\notin K$，因此$hk\notin H\cup K$.但$h,k\in H\cup K$，与$H \cup K \le G$矛盾
因此$H\sube K\vee K\sube H$

• 因此，子群的并集不一定是子群

6.1.5 循环群

定义

设$G$是群，若$\exists a \in G$使得$G=\{ a^{k}|k\in Z \}$，则称$G$是循环群，记作$G=\langle a \rangle$，称$a$为$G$的生成元

• eg:对于任何群$G$，由$G$中元素$a$生成的子群是循环群
  • 有限循环群中所有元素都是有限阶，且互不相等
  • 无限循环群中所有元素都是无限阶，且互不相等（除单位元$e$外）

分类

$G=\langle a \rangle$，根据$|a|$分为两类：

• 若$a$是$n$阶元，则

$$G=\{a^0=e,a^1,a^2,...,a^{n-1}\}$$

则 $|G|=|a|=n$，称$G$为$n$阶有限循环群

• 若$a$是无限阶元，则

$$G=\{a^0=e,a^{\pm1},a^{\pm2},...\}$$

则称$G$为无限循环群

由$a$生成的循环群只有一个生成元吗？
$<Z,+>=\langle 1 \rangle=\langle -1 \rangle$
$<Z_{4},\oplus_{4}>=\langle 1 \rangle=\langle 3 \rangle$

循环群的生成元求法

设$G=\langle a \rangle$是循环群

• 若$G$是无限循环群，则$G$只有两个生成元$a、a^{-1}$
• 若$G$是$n$阶循环群，则$G$有$\phi(n)$个生成元
  （1）对于任何小于$n$且与$n$互质的正整数$r$，$a^{r}$是$G$的生成元
  （2）$\phi(n)$欧拉函数：对于任何正整数$n$，小于$n$且与$n$互质的正整数个数
  eg:$\phi(12)=4(1,5,7,11)$

$$|a^{i}|=\frac{lcm(n,i)}{i}=\frac{n}{gcd(n,i)}$$

循环群的子群求法

设$G=\langle a \rangle$是循环群

• $G$的子群仍然是循环群
• 无限循环群$G$的子群除了$\{e\}$外都是无限循环群

$\langle a^{m}\rangle \le G,m\in Z. 取t\not = m ,\langle a^{m}\rangle \not = \langle a^{t}\rangle$

• $n$阶循环群$G$，对于$n$的每个正因子$d$，$G$恰好含有一个$d$阶子群$H=\langle a^{n/d}\rangle$

例:求出下列$G$的子群
（1）$G=\langle a \rangle$为无限循环群

$\langle e\rangle=\{e\}$
$\langle a\rangle=\langle a^{-1}\rangle=G$
$\langle a^{2}\rangle=\langle a^{-2}\rangle=\{e,a^{\pm2},a^{\pm4},a^{\pm6},...\}$
…

（2）$G$为12阶循环群$\langle a \rangle$

12的正因子有1,2,3,4,6,12.$G$有6个子群
$\langle e\rangle=\{e\}$
$\langle a\rangle=\{G\}$
$\langle a^{2}\rangle=\{e,a^{2},a^{4},a^{6},a^{8},a^{10}\}$
$\langle a^{3}\rangle=\{e,a^{3},a^{6},a^{9}\}$
$\langle a^{4}\rangle=\{e,a^{4},a^{8}\}$
$\langle a^{6}\rangle=\{e,a^{6}\}$

6.1.6 n元置换群

循环群都是Abel群，置换群一般不是

定义

设$S=\{1,2,...,n\}$，$s$上的任何双射函数$\sigma：S\rightarrow S$称为$S$上的$n$元置换，$(1)$表示恒等置换。即：

$$\sigma= \begin{pmatrix} 1 & 2 & ... & n\\ \sigma(1) & \sigma(2) & ... & \sigma(n) \end{pmatrix}$$

• 所有的$n$元置换构成的集合$S_{n}$，其关于置换的乘法封闭，置换的乘法满足结合律，恒等置换(1)是$S_{n}$中的单位元，对于任何$n$元置换$\sigma \in S_{n}$，逆置换$\sigma^{-1}$是$\sigma$的逆元。因此$S_{n}$关于置换的乘法构成一个群，称为n元对称群，其子群称为n元置换群。

乘法与逆

两个$n$元置换的乘法就是函数的符合运算，$n$元置换的求逆就是求反函数

$$\sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 5 & 3 & 2 & 1 & 4 \end{pmatrix},\tau=\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 4 & 3 & 1 & 2 & 5 \end{pmatrix}\\ \sigma^{-1}= \begin{pmatrix} 5 & 3 & 2 & 1 & 4\\ 1 & 2 & 3 & 4 & 5 \end{pmatrix}=\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 4 & 3 & 2 & 5 & 1 \end{pmatrix}\\ \sigma\tau=\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 1 & 2 & 5 & 3 & 4 \end{pmatrix}$$

轮换与对换

设$\sigma$是$S=\{1,2,...,n\}$上的$n$元置换，若$\sigma(i_{1})=i_{2},\sigma(i_{2})=i_{3},...,\sigma(i_{k-1})=i_{k},\sigma(i_{k})=i_{1}$，且保持$S$中其他元素不变，则称$\sigma$为$S$上的$k$阶轮换，记作$(i_{1}i_{2}...i_{k})$。若$k=2$，则称$\sigma$为$S$上的对换。
如

$$\sigma=\begin{pmatrix} 1 & 2 & 3 & 4 & 5\\ 5 & 3 & 2 & 1 & 4 \end{pmatrix}=(1\space 5\space 4)(2\space 3)=(1\space 4)(1\space 5)(2\space 3)$$

任何$n$元置换都可以唯一地表示成不相交的轮换之积，而任何轮换都能表示为对换之积

$$(i_{1}i_{2}...i_{k})=(i_{1}i_{k})...(i_{1}i_{3})(i_{1}i_{2})$$

• $n$元置换的对换表达式不唯一，但表达式中所含对换个数的奇偶性不变
  • 如4元置换$\tau=(1\space 2 \space 3 \space 4)$只能表示为奇数个对换之积
• $n$元置换可以表示为奇数个对换之积，则称为奇置换，否则称为偶置换，奇偶置换各有$n!/2$个。

置换的阶

$G$是$n$元置换群

• k阶轮换的阶是k
• 置换的阶是各轮换阶的最小公倍数
  • 例1：$\tau=\begin{pmatrix}1&2&3&4&5&6&7&8\\ 5&2&3&8&7&6&1&4\end{pmatrix}$
    易知$|\tau|=[|(1\space 5\space 7)|,|(4\space 8)|]=[3,2]=6$
  • 例2：$(1\space 2\space 4\space 3)(3\space 5\space 8)(6\space 7)$的阶是？是奇置换/偶置换？
    $|(1\space 2\space 4\space 3)(3\space 5\space 8)(6\space 7)|=|\begin{pmatrix}1&2&3&4&5&6&7&8\\2&4&5&3&8&7&6&1\end{pmatrix}|=|(1\space 2\space 4\space 3\space 5\space 8)(6\space 7)|=[6,2]=6$
    因此阶为6，是偶置换

6.1.7 群的分解

拉格朗日定理

设$G$是有限群，$H$是$G$的子群，则$|G|=[G:H]\cdot|H|$
$[G:H]$是$H$在$G$中的指数

• 推论：设$G$是$n$阶群，则$\forall a\in G$，$|a|$是$n$的因子，且有$a^{n}=e$
• $\langle a\rangle$是$G$的子群，阶是$n$的因子

推论和应用

• 素数阶群都是循环群
• 6阶群中必含有3阶元、2阶元
• 6阶群在同构意义下只有2个
• 4阶群在同构意义下只有2个

6.2 环

6.2.1 环

定义

环是具有两个二元运算的代数系统，分别称为加法和乘法，记作$+$和$\cdot$
设$\langle R,+,\cdot\rangle$是具有两个二元运算的代数系统，如果

• $\langle R,+\rangle$构成Abel群
• $\langle R,\cdot\rangle$构成半群
• $\cdot$对$+$满足分配律

则称该代数系统是环。环中加法和乘法的单位元记作0和1（1可能不存在），环中元素的加法逆元称为负元，记作$-x$；$x$的乘法逆元如果存在称为逆元，记作$x^{-1}$。类似的，将$x+(-y)$记作$x-y$

（1）整数集、有理数集、实数集和复数集关于普通加法和乘法构成环，分别称为整数环$Z$、有理数环$Q$、实数环$R$和复数环$C$
（2）$n(n>2)$阶实矩阵的集合$M_{n}(R)$关于矩阵加法和乘法构成n阶实矩阵环
（3）幂集$P(B)$关于集合的对称差和交运算构成环$\langle P(B),\oplus,\cap\rangle$
（4）$\langle Z_{n},\oplus,\otimes\rangle$构成环，称为模n的整数环
（5）设$\langle G,\circ\rangle$是Abel群，在$G$上定义$*：\forall x,y\in G,x*y=e$，则$\langle G,\circ,*\rangle$构成零环

运算性质

• $0a=a0=0$

$a0=a(0+0)=a0+a0$，由消去律得$a0=0$
$0a=(0+0)a=0a+0a$，由消去律得$0a=0$
故$0a=a0=0$

• $(-a)b=a(-b)=-ab$

$(-a)b+ab=(-a+a)b=0b=0$
$ab+(-a)b+=(-a+a)b=0b=0$
因此$(-a)b$是$ab$的加法逆元$\Rightarrow (-a)b=-ab$
同理，$a(-b)$是$ab$的加法逆元$\Rightarrow a(-b)=-ab$
由逆元的唯一性，$(-a)b=a(-b)=-ab$

• $(-a)(-b)=ab$

由$(-a)b=a(-b)$，$(-a)(-b)=(-(-a))b=ab$

• $(a-b)c=ac-bc$

$(a-b)c=(a+(-b))c=ac+(-b)c=ac-bc$

• $c(a-b)=ca-cb$

$c(a-b)=c(a+(-b))=ca+c(-b)=ca-cb$

• $\sum_{i=1}^{m}a_{i}\sum_{j=1}^{n}b_{j}=a_1b_1+...a_1b_n+...+a_mb_1+...+a_mb_n$

$\sum_{i=1}^{m}a_{i}\sum_{j=1}^{n}b_{j}=(a_1+a_2+...+a_m)(b_1+b_2+...b_n)=a_1(b_1+b_2+...b_n)+a_2(b_1+b_2+...b_n)+...+a_m(b_1+b_2+...b_n)=a_1b_1+...a_1b_n+...+a_mb_1+...+a_mb_n$

• $\forall a,b\in R,n\in Z,(na)b=a(nb)=n(ab)$

证明略

例 在环中计算$(a+b)^3,(a-b)^2$
$(a+b)^3=a^3+ba^2+aba+b^2a+a^2b+bab+ab^2+b^3$
$(a-b)^2=(a-b)(a-b)=a^2-ba-ab+b^2$

6.2.2 环中的零因子

定义

设$\langle R,+,\cdot\rangle$是环，若$\exists ab=0$，且$a\not =0,b\not =0$，则称$a$为左零因子，$b$为右零因子(此处的0指环中加法的单位元)，即两个非0元素的乘积为0，这样的元素称为左/右零因子
如$\langle Z_{6},\oplus,\otimes\rangle$，其中$2\otimes 3=0$，2和3都是零因子，这个环含有零因子，不是无零因子环
无零因子的条件：$ab=0\rightarrow a=0\lor b=0$

• 定理：在一个没有零因子的环里两个消去律成立。反之一个环里消去律成立，则这个环没有零因子：

$$a\not =0,ab=ac\rightarrow b=c\\ a\not =0,ba=ca\rightarrow b=c$$

证明：由于R中没有零因子，因此由$a\not =0$和

$$ab=ac\rightarrow ab-ac=0\rightarrow a(b-c)=0$$

得$b-c=0$，即$b=c$消去律成立
反之，假设消去律成立，因为$ab=0\rightarrow ab=a0$
由消去律$a\not =0$则$b=0$，因此环$R$中没有零因子

定理：一个环中若有一个消去律成立，则另一个消去律也成立

6.2.3 特殊的环

定义

设$\langle R,+,\cdot\rangle是环$

• 若环中$\cdot$适合交换律，则$R$是交换环
• 若环中$\cdot$存在单位元，则$R$是含幺环
• 若$\forall a,b\in R,ab=0\rightarrow a=0\lor b=0$，则称$R$是无零因子环
• 若$R$交换、含幺、无零因子，则$R$是整环

6.2.4 除环和域

若$R$为环，$|R|>1$，令$R^{*}=R-{0}$，且$R^{*}$构成群，则称$R$是一个除环
若$R$为交换环，满足以上除环的条件，则称R为域
一个域$F$是具有两个二元运算的代数系统，其中$F$与加法构成Abel群，$F^{*}=F-{0}$与乘法也构成Abel群

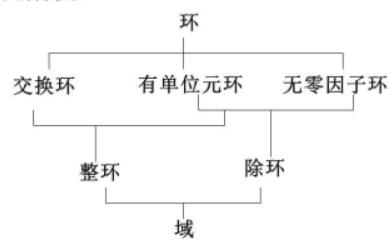
（1）整数环$Z$、有理数环$Q$、实数环$R$中的乘法适合交换律、含有单位元1、不含零因子，因此是交换环、含幺环、无零因子环和整环。其中有理数环和实数环是域（除0外均有逆元）
（2）n阶实矩阵环$\langle M_{n}(R),+,*\rangle$不是交换环，是含幺环（单位元是$n$阶单位矩阵），不是无零因子环，因此也不是整环和域
（3）模n的整数环$\langle Z_{n},\oplus,\otimes\rangle$是交换环、含幺环，当$n$为质数时构成无零因子环、整环和域；当$n$为合数时构成不构成整环和域

6.3 格与布尔代数

格与布尔代数均是加载有两个二元运算的代数系统，布尔代数也是一种格

6.3.1 格

定义

设$\langle S,\preccurlyeq \rangle$是偏序集，若$\forall x,y\in S,\{x,y\}$均有上确界和下确界，则称$S$关于$\preccurlyeq$构成格
其中，求上确界记作$\lor$，下确界记作$\land$

对偶原理

设$f$是含有符号$=,\preccurlyeq \succcurlyeq \lor \land$的公式，令$f^{*}$为$f$中的$\lor \rightarrow\land,\preccurlyeq\rightarrow\succcurlyeq...$后的对偶式，若$f$为真，则$f^{*}$也为真

一些性质

$\langle L,\preccurlyeq \rangle$为格

• $\lor,\land$适合交换律，结合律，幂等律，吸收律
  • 吸收律：$\forall a,b\in L$，有$a\lor(a\land b)=a,a\land(a\lor b)=a$

格的等价定义：

• $\langle S,*,\cdot \rangle$是代数系统，如果$*$和$\cdot$满足交换律、结合律、吸收律，则 $\langle S,*,\cdot \rangle$构成格

证幂等律：
$\forall a \in S,a*a=a*(a\cdot(a*a))=a$
同理有$a\cdot a=a$

子格

设$L$为格，$S$是$L$的非空子集，如果$S$关于$L$中的运算封闭，则称$S$是$L$的子格

特殊的格

1）分配格

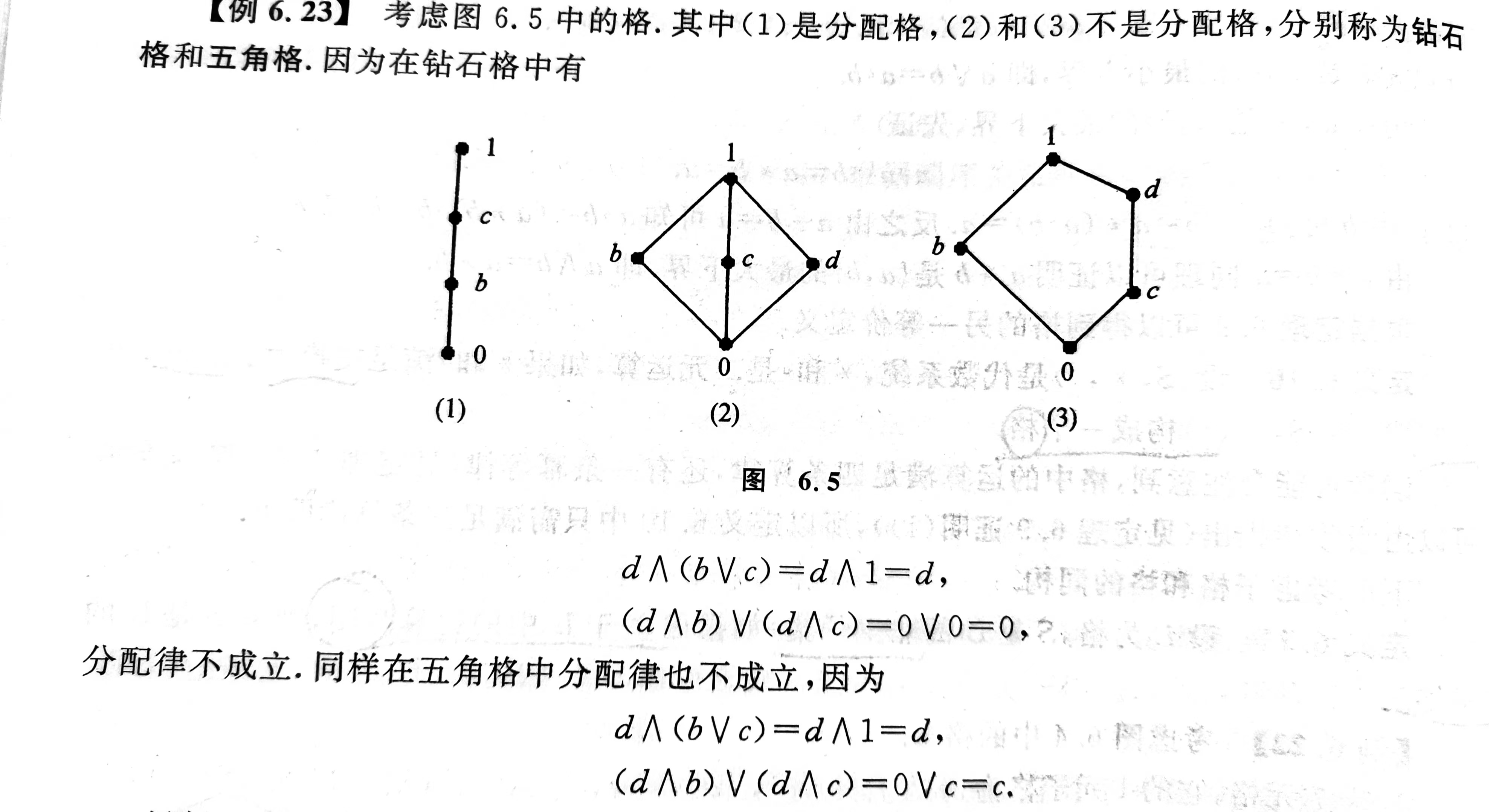
• $L$是分配格当且仅当不含有与钻石格和五角格同构的子格
• 所有的链都是分配格
• 元数小于5的格都是分配格

2）有界格
如果一个格存在全下界$a$（$\exists a\in L,\forall b\in L\rightarrow a\preccurlyeq b$）和全上界$c$（$\exists c\in L,\forall b\in L\rightarrow b\succcurlyeq c$），则为有界格，记作$\langle L,\land,\lor,0,1\rangle$

• 有限格都是有界格
• 幂集格$P(B)$都是有界格，$1=B,0=\phi$；群$G$的子群格是有界格，$1=G,0=\{e\}$

3）有补格
设$\langle L,\land,\lor,0,1\rangle$是有界格，$a\in L$，若$\exists b\in L$满足$a\land b=0,a\lor b=1$，则称$b$是$a$的补元。若每个元素都有补元则为有补格

• 分配格中，补元一定唯一

设$L$是分配格，$a\in L$，假设$a$存在补元$b$和$c$，则

$$a\land b=0=a\land c,a\lor b=1=a\lor c$$

由分配格性质，$b=c$

4）布尔格
有补分配格称为布尔格（布尔代数）

• 幂集$\langle P(B),\cap,\cup,',0,1\rangle$是布尔格
• 钻石格和五角格不是布尔格
• 长度大于2的链也不是布尔格

等价定义：
设$\langle B,*,\cdot\rangle$是代数系统，如果$*$和$\cdot$满足：

• 交换律，$\forall a,b\in B,a*b=b*a,a\cdot b=b\cdot a$
• 分配律，$\forall a,b,c\in B,a*(b\cdot c)=(a*b)\cdot(a*c),a\cdot(b* c)=(a\cdot b)*(a\cdot c)$
• 同一律，$\exists 0,1\in B,\forall a\in B,a*1=a,a\cdot 0=a$
• 补元律，$\forall a\in B,\exists a'\in B\rightarrow a*a'=0,a\cdot a'=1$

则称$\langle B,*,\cdot\rangle$是布尔代数