形式语言与自动机考试例题整理
1.构造DFA/NFA
$L=\lbrace x|x\in\lbrace 0,1\rbrace ^{+}且x满足…\rbrace $
-
以01、101、1101开头
DFA:要注意$q_{die}$状态的设计。以101为例,DFA如下:
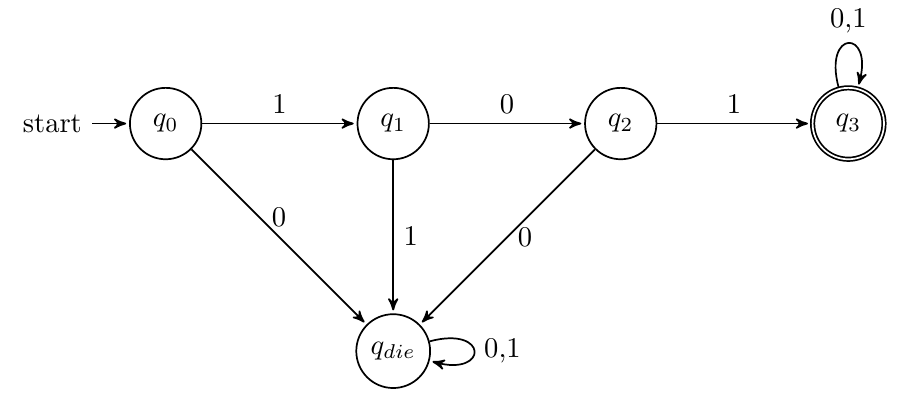
-
包含01、101、1101
DFA:先把包含该串的状态画出来,再考虑其他转移状态的设计
NFA:从每个字母开始猜测
以1101为例,DFA和NFA如下:
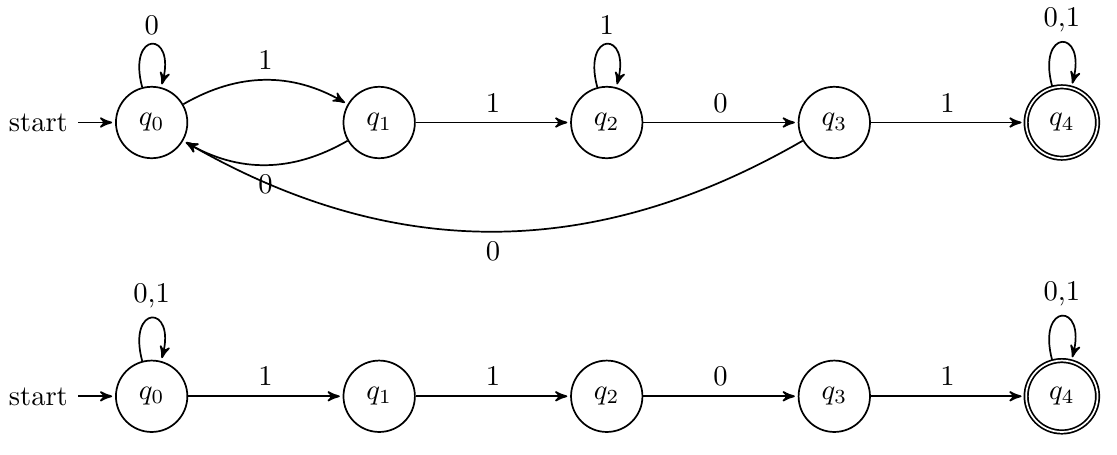
-
以01、101、1101结尾
DFA:先把该串状态画出来,再考虑其他转移状态的设计
NFA:从每个字母都开始猜测
以1101为例,DFA和NFA如下:
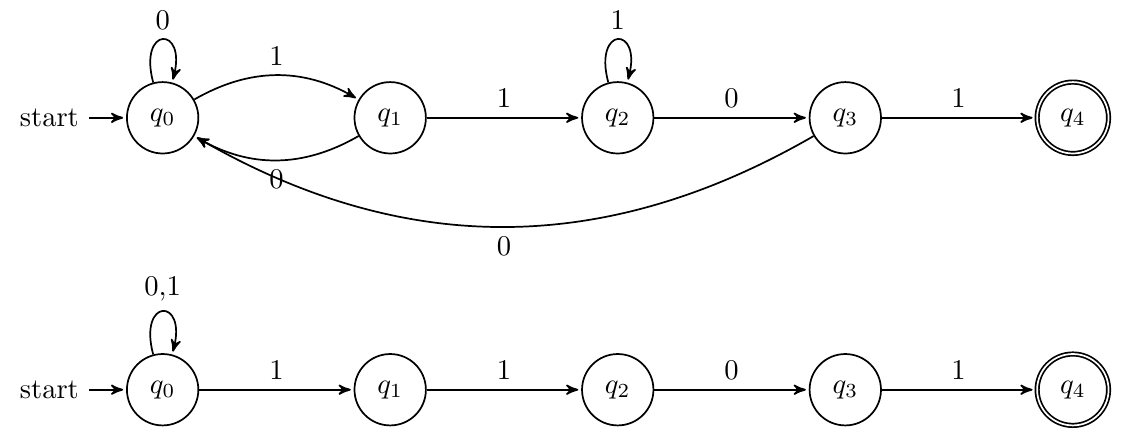
-
不包含00、11、1010
DFA:直接将
包含00、11、1010情况中DFA的非接受状态和接受状态互换即可 -
同时含有01和10
- DFA:考虑将首字母分为0/1分别讨论
- NFA:在每个字母的位置分0和1进行猜测即可
-
同时含有00和11
-
把$x$看做二进制时,$x$模5余3
先看一道书上的例题,P36 2.2.6(a):
x以1开头,解释为二进制整数时是5的倍数,如101、1010、1111
-
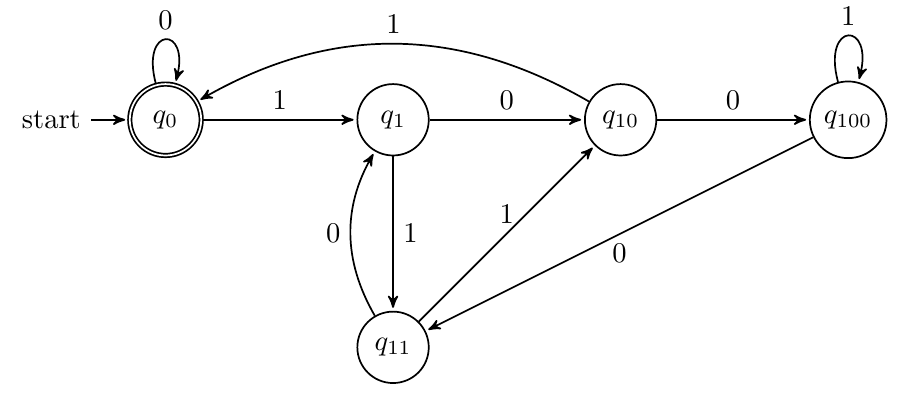
先不看以1开头,由于任何整数模5,其余数都在0到4之间。我们考虑只针对余数设计状态间转移,即$q_{0}/q_{1}/q_{10}/q_{11}/q_{100}$四个状态,$q_0$为接受状态。转移规则如下:假设我们当前读到的01串是$(y)_2=(5a+b)_{10},0\le b\le 4$,那么$(y1)_2=(10a+2b+1)_{10},(y0)_2=(10a+2b)_{10}$,其中$y1$需要判断$2b+1$是否$\le 5$,即识别到1余数$\times2+1$,识别到0余数$\times 2$
-
加入以1开头,即进入该转移的初始状态为$q_1$,我们可以增加一个初始状态$q_s$,接收0则进入状态$q_{die}$,接收1则进入$q_1$
回到此题,显然以$q_{11}$作为接受状态即可。
如果此题说x是5的倍数的二进制表示,需要考虑判断是否有前缀0,如0000101,不被接受
-
-
$x$以1结尾,长度为偶数;以0结尾,长度为奇数
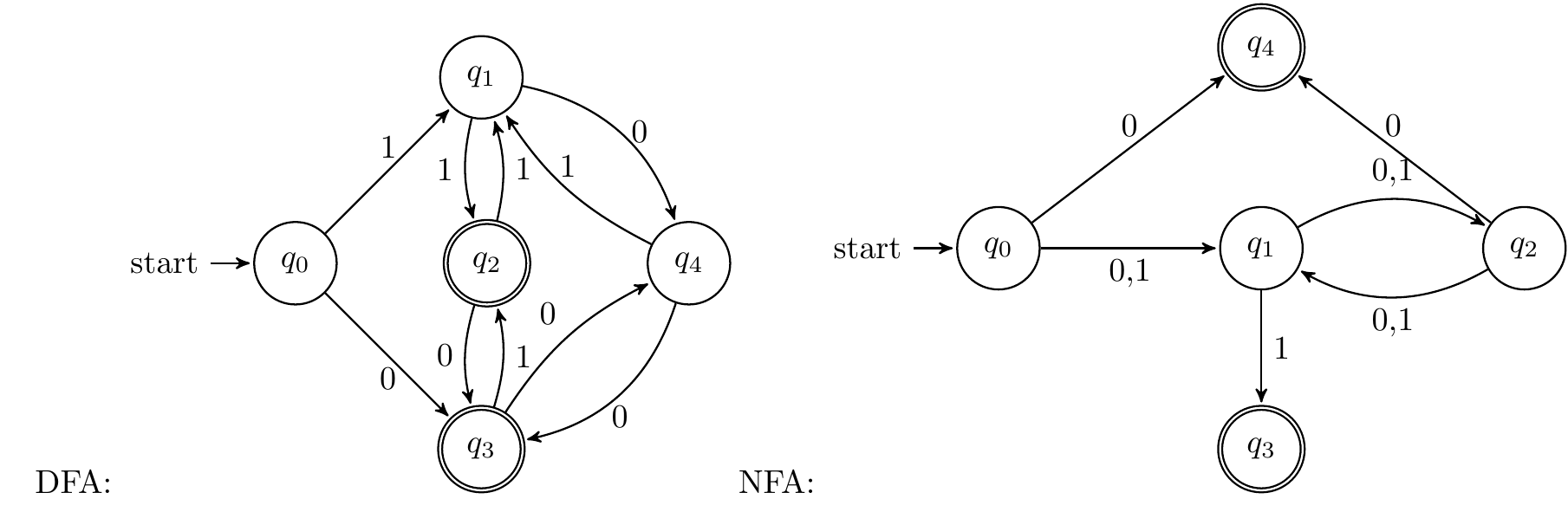
- DFA:可以考虑四个状态,1结尾长度为奇数、1结尾长度为偶数、0结尾长度为奇数、0结尾长度为偶数,可添加一个初始状态,然后在四个状态间进行转移即可
- NFA:先考虑设计奇数、偶数两个状态,奇数状态尝试再识别1达到接受状态,偶数状态尝试再识别0达到接受状态
-
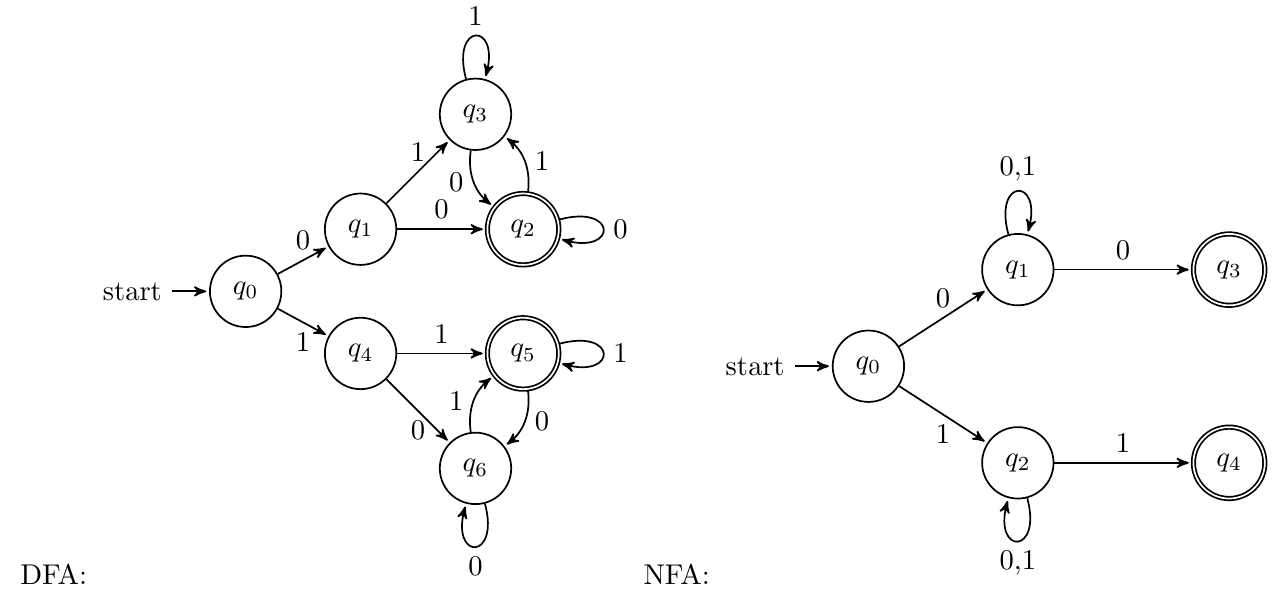
$x$的首字符和尾字符相等
分01讨论即可
-
$x$是十进制非负数
不接受有前缀0的即可(单个0除外)
-
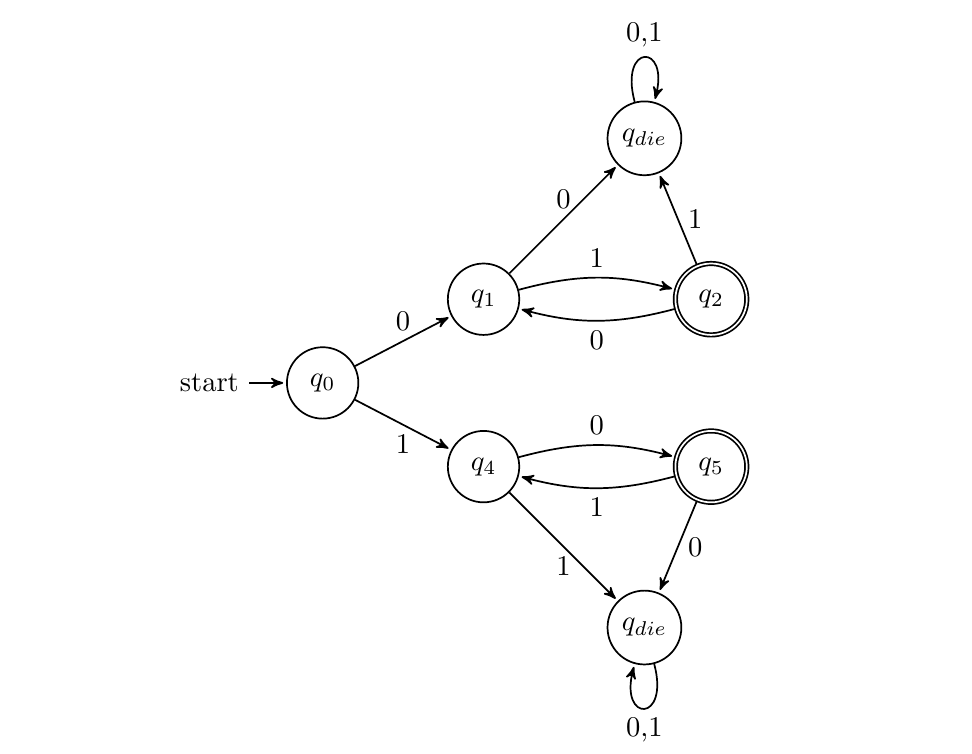
$x$中0和1个数相等且交替出现
分第一个元素为0/1讨论即可,DFA如下:
-
$x$中0的个数被2整除,1的个数被3整除
不在考试范围内,可考虑对0构造状态$q_{00},q_{01}$,对1构造状态$q_{10},q_{11},q_{12}$,从而构造出$2\times3=6$个状态,接受状态为$q_{00}q_{10}$
-
$x$以01开头或以01结尾(含同时)
DFA:
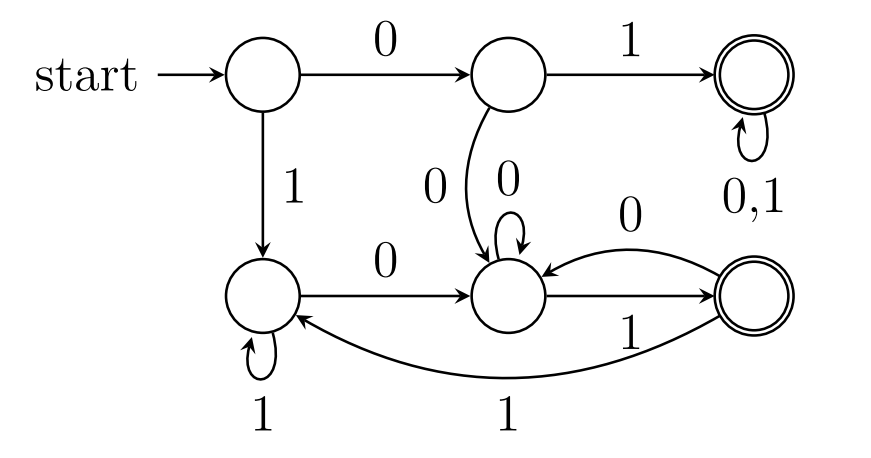
NFA:
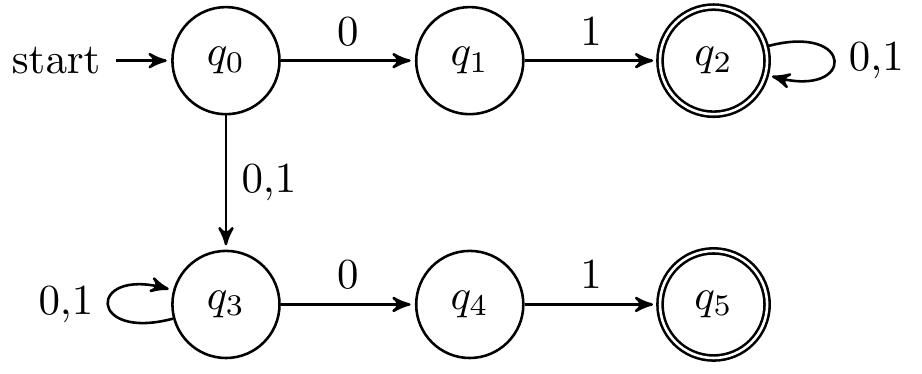
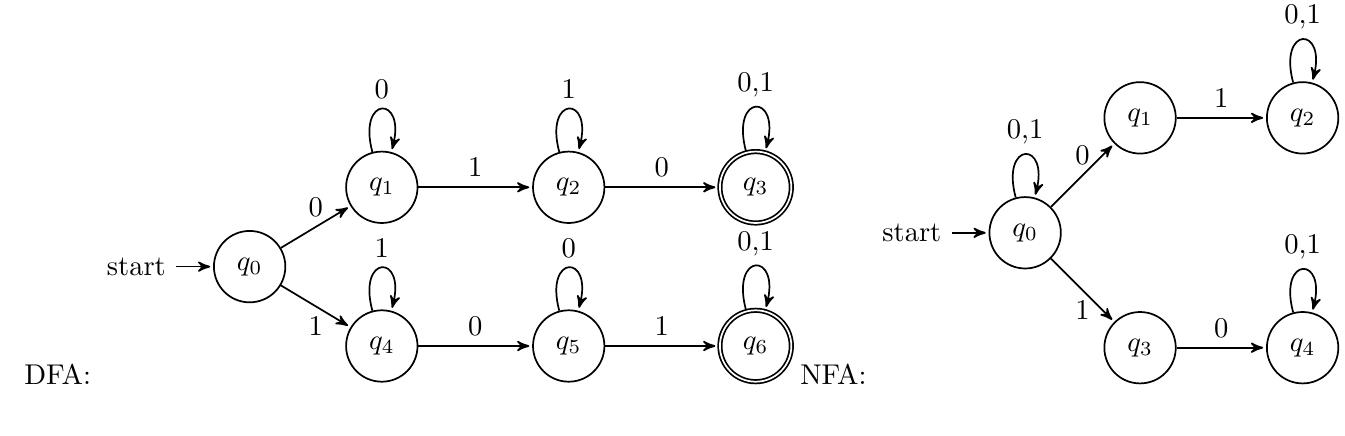
- $x$倒数3个字符至少有一个是1
NFA:三种方式均可,第二个NFA可以认为是在x倒数第3个字符是1的基础上得到
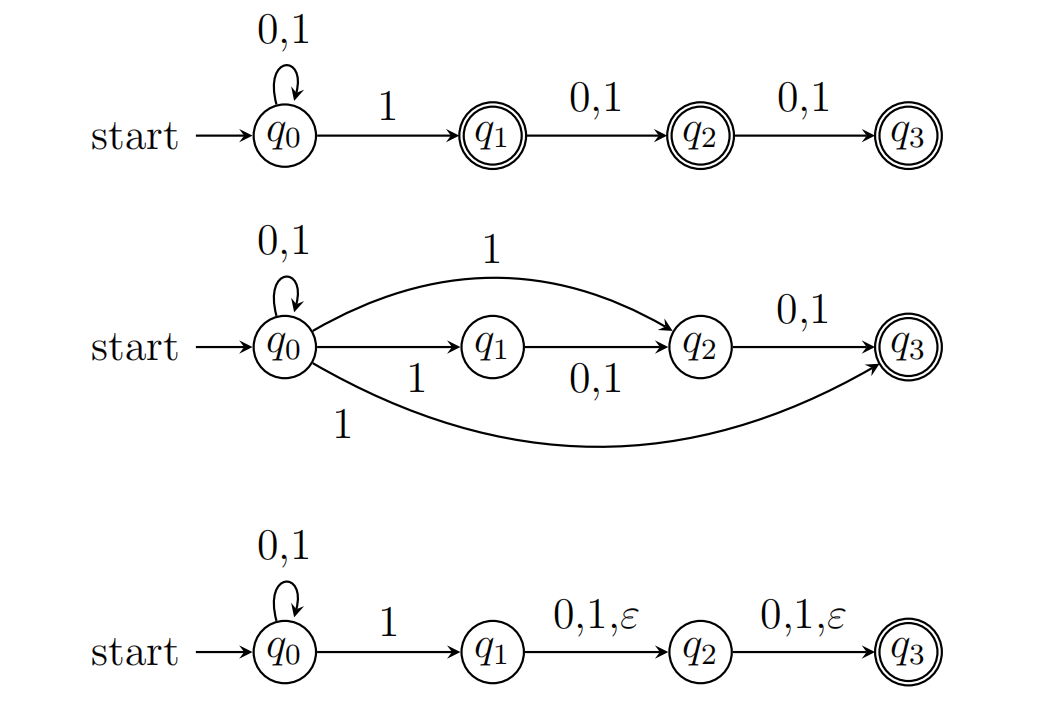
2.DFA算法
2.1 $\epsilon$-NFA2NFA
2.2 NFA2DFA
采用子集构造法
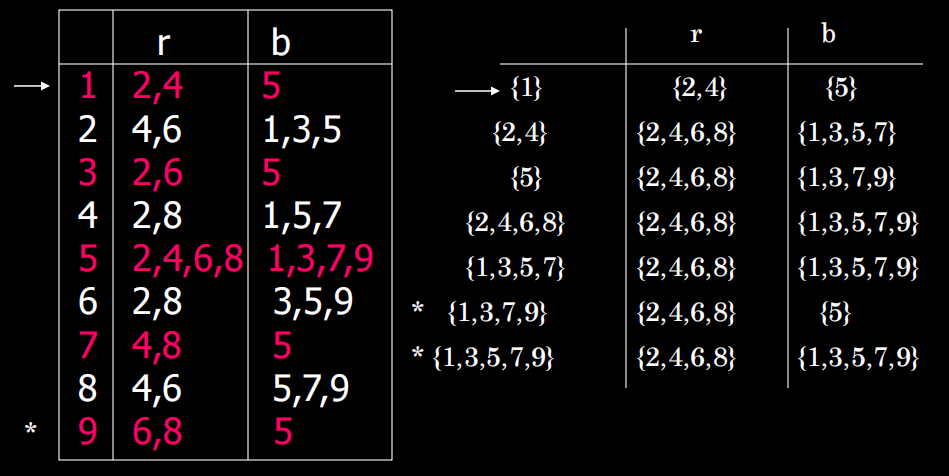
2.2 等价性Equivalence
考的概率比较小,用于判断两个DFA是否定义了相同的语言。方法:构造乘积自动机(product DFA)、填表法
-
乘积自动机
状态集分别为$Q,R$,乘积$DFA$状态集为$Q\times R,[q,r]$,其中$q\in Q,r\in R$
注意:
-
当且仅当自动机$L$和$R$中只有一个接受$w$时,标记为接受状态
-
当该自动机的语言为空时,两个自动机等价
-
-
填表法
注意:当初始状态等价时,自动机等价
2.3 最小化Minimally
用于找出最少状态的DFA或最短长度的RE,方法:消除不可达状态,合并不可区分状态
- 采用填表法,合并不可区分状态
填表法步骤示例:
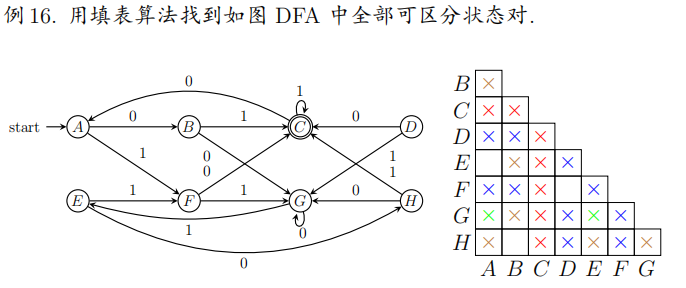
- 直接标记终态和非终态之间的状态对:$\lbrace C\rbrace $$\times$$\lbrace A,B,D,E,F,G,H\rbrace $
- 标记所有经过字符 0 到达终态和非终态的状态对:$\lbrace D,F\rbrace $$\times$$\lbrace A,B,C,E,G,H\rbrace $
- 标记所有经过字符 1 到达终态和非终态的状态对:$\lbrace B,C,H\rbrace $$\times$$\lbrace A,C,D,E,F,G\rbrace $
- 检查剩下状态对:$[A,G],[E,G]$可区分
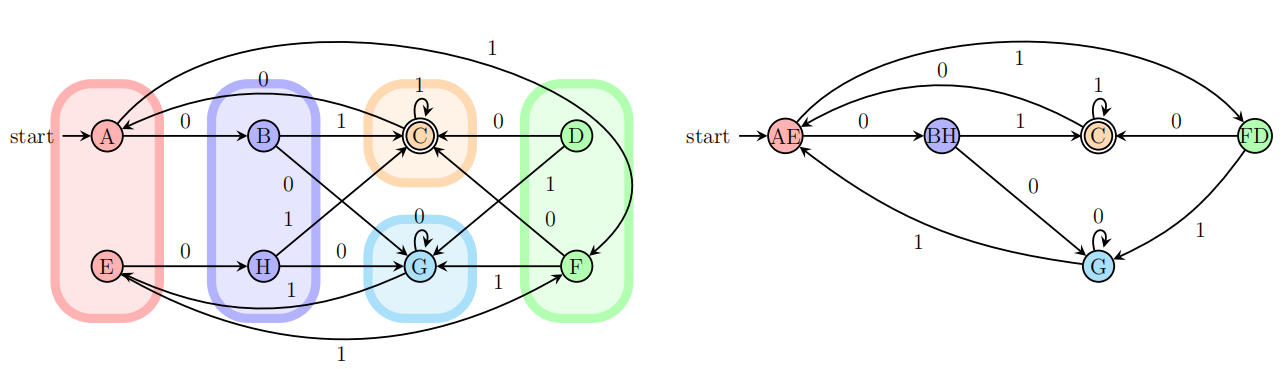
3.正则表达式
3.1 语言写正则表达式
分治法、递归、串接等方法设计正则表达式
$L=\lbrace w|w\in \lbrace a,b,c\rbrace^{*},且w至少包含一个a和一个b\rbrace $
分$a$和$b$的先后顺序即可
$$ c^{*}a(a+c)^{*}b(a+b+c)^{*} + c^{*}b(b+c)^{*}a(a+b+c)^{*} $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},且倒数第三个符号是1\rbrace $
$$ (0+1)^{*}1(0+1)(0+1) $$
$L=\lbrace w|w\in \lbrace 0,1\rbrace ^{*},w没有两个连续的0\rbrace $
对于此类问题,有两种方法:
-
利用式子$\sum^{*}=(0+1)^{*}$,该式认为$00101=((0)(0)(1)(0)(1))$。我们只要让0产生的时候跟一个1即可,同时需要注意末尾和开头的0/1、以及满足空串的要求 $$ (1+01)^{*}(0+\epsilon)或(0+\epsilon)(1+10)^{*} $$
-
利用式子$\sum^{*}=(0^{*}1^{*})^{*}$,该式子认为$0011011=((00)(11))((0)(11))$。同理我们产生0时加上1即可,同时需要注意空串和前后0/1的要求 $$ 1^{*}(011^{*})^{*}(0+\epsilon) $$
$L=\lbrace w|w\in \lbrace 0,1\rbrace ^{*},w没有两个连续的1\rbrace $
参考上一问: $$ (0+10)^{*}(1+\epsilon)或(1+\epsilon)(0^{*}01)^{*}0^{*} $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},且w至多只有一对连续的1\rbrace $
没有连续的1或者有一对连续的1
错误示范: $$ (0+10)^{*}(1+\epsilon)+(1^{*}0+\epsilon)11(01^{*}+\epsilon) $$
正确示范: $$ (0+10)^{*}(1+\epsilon)+(0+10)^{*}11(0+01)^{*} $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},且w有两对连续的1\rbrace $
case 1: 111的形式 $$ (0+10)^{*}111(0+01)^{*} $$ case 2:11..11的形式 $$ (0+10)^{*}11(0+0(1+\epsilon)(0+01)^{*}0)11(0+01)^{*} $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},w中每对相邻的0都在任何一对相邻的1前面\rbrace $
问题等价为没有连续的1串接上没有连续的0 $$ (0+10)^{*}(\epsilon +1)(1+01)^{*}(0+\epsilon) $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},w中不包含子串01\rbrace $
$$ 1^{*}0^{*} $$
$L=\lbrace w|w\in\lbrace 0,1\rbrace ^{*},w中不包含子串10\rbrace $
$$ 0^{*}1^{*} $$
3.2正则表达式写语言
较简单,无例题
3.3(非考试)正则表达式转NFA
-
对于$r+s$,
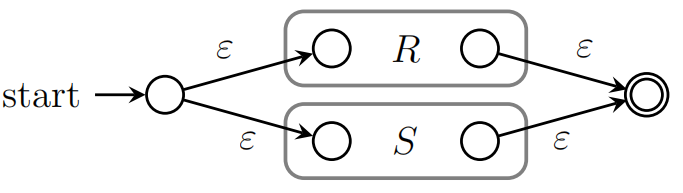
-
对于$rs$,有

-
对于$r^{*}$,有
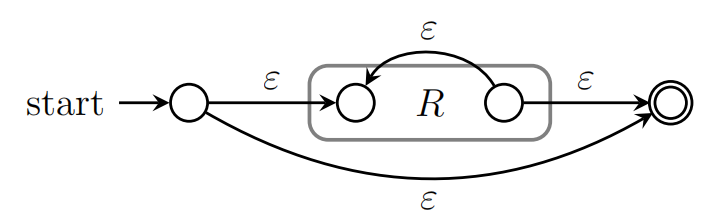
4.上下文无关文法CFG
4.1 构造CFG
给出$L=\lbrace 0^n1^n|n\ge 0\rbrace $的文法
$$ S\rightarrow 0S1|\epsilon $$
给出$L=\lbrace 0^n1^n|n\ge 1\rbrace $的文法
$$ S\rightarrow 0A1\ A\rightarrow 0A1|\epsilon $$
给出$L=\lbrace 0^n1^n0^m1^m|n\ge 0,m\ge 0\rbrace $的文法
$$ S\rightarrow AA\ A\rightarrow 0A1|\epsilon $$
给出$L=\lbrace 0和自然数(不能以0开头)\rbrace $
$$ S\rightarrow 0|AB\ A\rightarrow 1|2|3|4|5|6|7|8|9\ B\rightarrow CB|\epsilon\ C\rightarrow 0|A $$
给出$L=\lbrace 0^n1^m0^m1^n|n\ge 0,m\ge 0\rbrace $的文法
$$ S\rightarrow 0S1|\epsilon|A\ A\rightarrow 1A0|\epsilon $$
为语言$L=\lbrace 0^n1^m|n\not = m\rbrace $设计文法
分为$n>m$和$n<m$两种情况
即$00\ 000\ 111$和$000\ 111\ 11$ $$ S\rightarrow AC|CB\ A\rightarrow A0|0\ C\rightarrow 0C1|\epsilon\ B\rightarrow 1B|1 $$
给出$L=\lbrace x|x包含两个相同的全0子串\rbrace $的文法
考虑分为三部分,Eg. (1001)(00110100)(10110) $$ S\rightarrow ABC\ A\rightarrow \epsilon|U1\ U\rightarrow 0U|1U|\epsilon\ C\rightarrow 1U|\epsilon\ B\rightarrow 0B0|0D0\ D\rightarrow 1U1|1 $$
给出$L=\lbrace w\in\lbrace 0,1\rbrace ^{*}|w包含至少3个1\rbrace $的文法
$$ S\rightarrow A1A1A1A\ A\rightarrow 0A|1A|\epsilon $$
给出$L_{eq}=\lbrace w\in \lbrace 0,1\rbrace ^{*}|w中0和1个数相等\rbrace $的文法
$S\rightarrow 0S1|1S0|\epsilon|SS$,寻找递归结构,用变量构造
$S\rightarrow S0S1S|S1S0S|\epsilon$,目标串这样构成,由变量定义变量 $$ S \rightarrow 0B | 1A\ A \rightarrow 0 | 0S | 1AA\ B \rightarrow 1 | 1S | 0BB $$
给出$L_1=\lbrace ww^R|w\in\lbrace 0,1\rbrace ^{*}\rbrace $的文法
$$ S\rightarrow 0S0|1S1|\epsilon $$
给出$L=\lbrace w|w=w^R,w\in\lbrace 0,1\rbrace ^{*}\rbrace $的文法
$$ S\rightarrow 0S0|1S1|0|1|\epsilon\ $$
给出$L=\lbrace a^ib^jc^k|i\not =j或j\not =k\rbrace $的文法
$A/D$产生0个及以上的$a/c$,$E$产生1个及以上的b
$B$先产生相同数量的$b,c$,然后要么产生$\ge1$的b,要么产生$\ge 1$的c;C同理
因此$AB$代表$j\not =k$,$CD$代表$i\not =j$ $$ S \rightarrow AB | CD\ A \rightarrow aA | ε\ B \rightarrow bBc | E | cD\ C \rightarrow aCb | E | aA\ D \rightarrow cD | ε\ E \rightarrow bE | b\ $$
给出$L=\lbrace w\in\lbrace 0,1\rbrace ^{*}|w不是ww形式\rbrace $的文法
O生成奇数长度的串(一定不是ww形式),$E$生成偶数长度的串
将$E$分为左右长度相等的串$wl$和$wr$,最坏情况下只存在一个位置有$wl[i]\not =wr[i]$
我们以这个位置为中心,进行左右推导,即使左右推导的结果相等,最终的串也不相等 $$ S \rightarrow E|O\ O \rightarrow 0 | 1 | COC\ E \rightarrow AB | BA\ A \rightarrow CAC | 0\ B \rightarrow CBC | 1\ C \rightarrow 0 | 1\ $$
给出$L=\lbrace w\in\lbrace 0,1\rbrace ^{*}|0的个数是1的个数的两倍\rbrace $的文法
$$ S\rightarrow S1S0S0S|S0S1S0S|S0S0S1S|\epsilon $$
4.2 推导CFG
给定字符串,写出其最左、最右或最短的推导
给定文法 $$ S\rightarrow A1B\ A\rightarrow 0A|\epsilon\ B\rightarrow 0B|1B|\epsilon $$ 给出串00101的最左/右推导
最左:$S\rightarrow A1B\rightarrow 0A1B\rightarrow 00A1B\rightarrow 001B\rightarrow 0010B\rightarrow00101B\rightarrow 00101$
最右:$S\rightarrow A1B\rightarrow A10B\rightarrow A101B\rightarrow A101\rightarrow 0A101\rightarrow 00A101\rightarrow 00101$
4.3 画语法树
给定字符串及文法规则,画出语法树。和4.1最左/右推导一致,不再给出例题
4.4 二义性
如果CFG能为某个句子生成多颗语法解析树,则称CFG是二义的( ambiguous )
如果题目要求证明文法具有二义性:给出两颗不同的语法解析树即可
5.下推自动机PDA
5.1 设计PDA
接受可以写成空栈方式$\epsilon ,Z_0/\epsilon$或终结状态方式$\epsilon ,Z_0/Z_0$
设计识别$L_{01}=\lbrace 0^n1^n|n\ge1\rbrace $的PDA
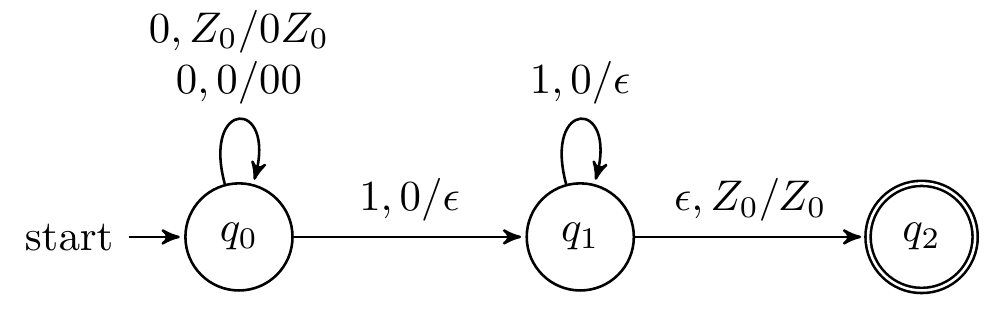
$L_{01}$识别符号串0011的动作序列?
$$ (q_0,0011,Z_0)\vdash(q_0,011,0Z_0)\vdash(q_0,11,00Z_0)\ \vdash(q_1,1,0Z_0)\vdash(q_1,\epsilon,Z_0)\ \vdash(q_2,\epsilon,Z_0) $$
设计识别$L_{wwr}=\lbrace ww^{R}|w\in (0+1)^{*}\rbrace $的PDA
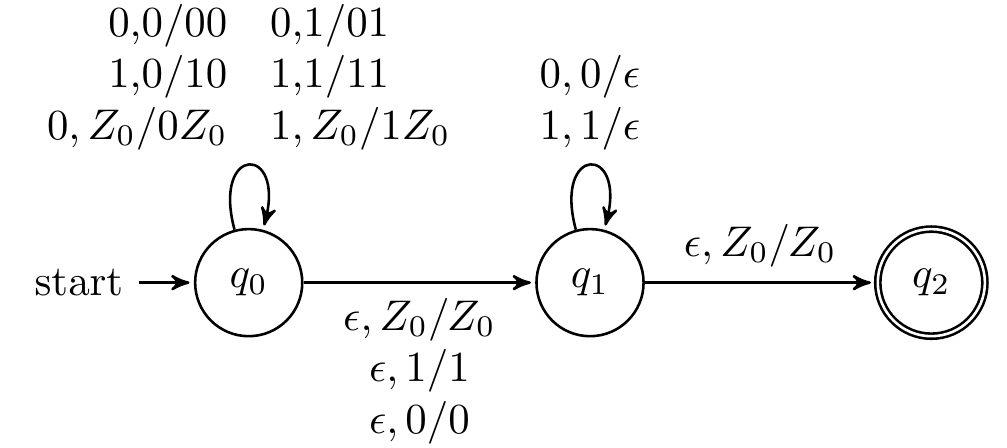
设计识别 $L_{w \# w r} = \lbrace w \# w^{R} \mid w \in (0+1)^{*} \rbrace$ 的 PDA
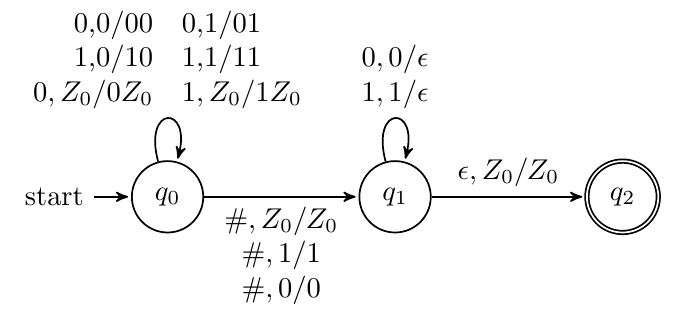
接受$L=\lbrace w:w=w^R|w\in (0+1)^{*}\rbrace $的PDA
对于奇数长度的串,选择跳过中间的0或1;对于偶数,不跳过(采用空转移实现)

接受$L=\lbrace w\in \lbrace 0,1\rbrace ^{*}|w中0和1的数量相同\rbrace $的PDA
对于01数量均为n的串,一定存在n个不相交的01匹配,因此可以用不确定的PDA实现
最后的$\epsilon,Z_0/\epsilon$是将栈底符号弹出,实现以空栈状态接受$w$
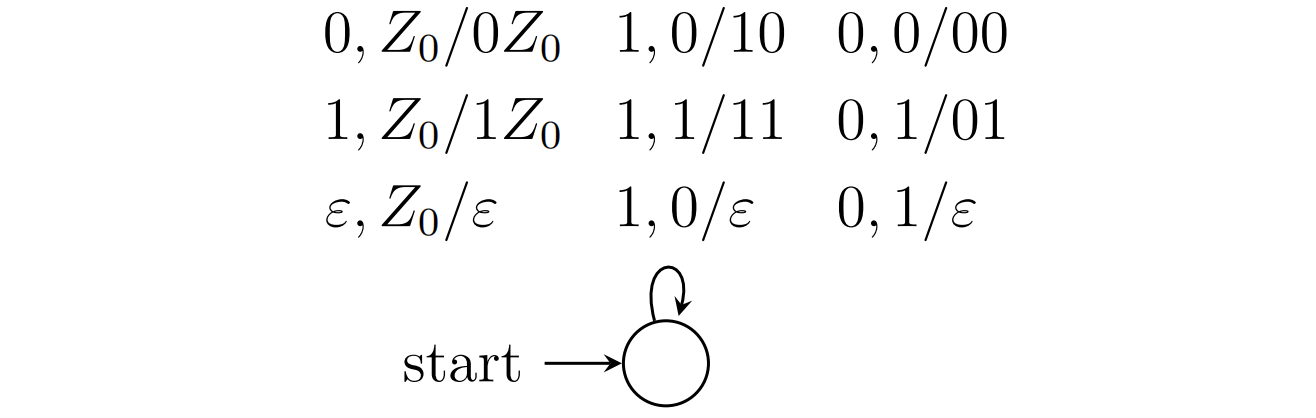
接受$L=\lbrace 0^n1^m|0\le n\le m\le 2n\rbrace $的PDA
由于每个0都对应1个1或者2个1,可以考虑将所有的0压栈,可以识别2个1再弹出0也可以识别出1个1再弹出0。对于识别2个1弹出0,我们增加一个状态,第一个1不弹0,第二个1弹出0
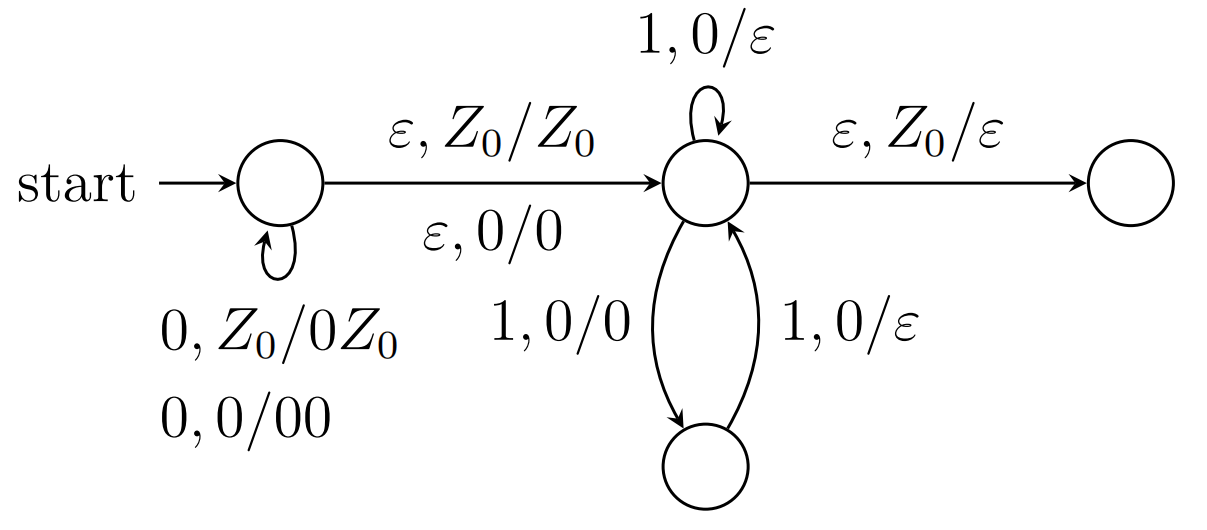
设计语言$L=\lbrace 0^n1^m|1\le m\le n\rbrace $的PDA
不出现$1,Z_0$即可
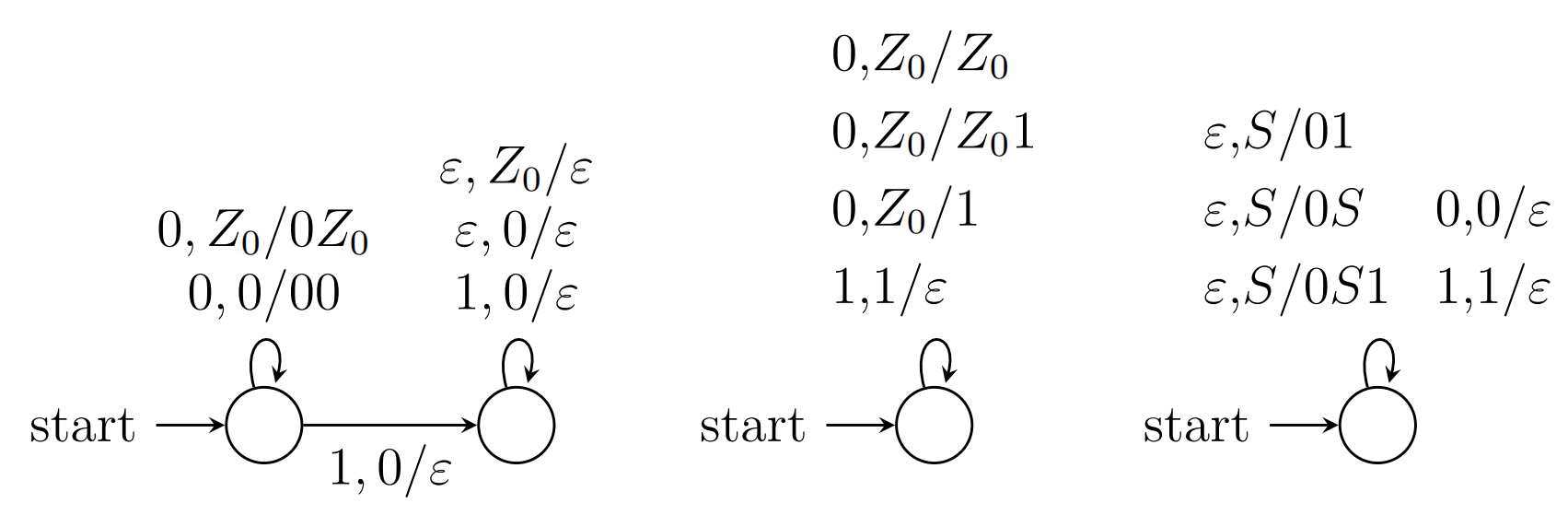
接受$L=\lbrace 0^n1^m0^m1^n|n\ge 0,m\ge 0\rbrace $的PDA
0压栈,1压栈,0弹出,1弹出,设计四个状态即可
接受$L=\lbrace w|w包含两个相同的全0子串\rbrace $的PDA
参考上文的CFG,(…1)(0…0)(1…1)(0…0)(1….)

5.2 根据CFG构造PDA
当$PDA$比较难写出来时,采用$CFG$转$PDA$的方法
如果$CFG\ G=(V,T,P’,S)$,构造$PDA$ $$ P=(\lbrace q\rbrace ,T,V\cup T,\delta,q,S,\phi) $$ 其中$\delta$为:
- $\forall A\in V$:$\delta(q,\epsilon,A)=\lbrace (q,\beta)|A\rightarrow\beta\in P’\rbrace $
- $\forall a\in T$:$\delta(q,a,a)=\lbrace (q,\epsilon)\rbrace $
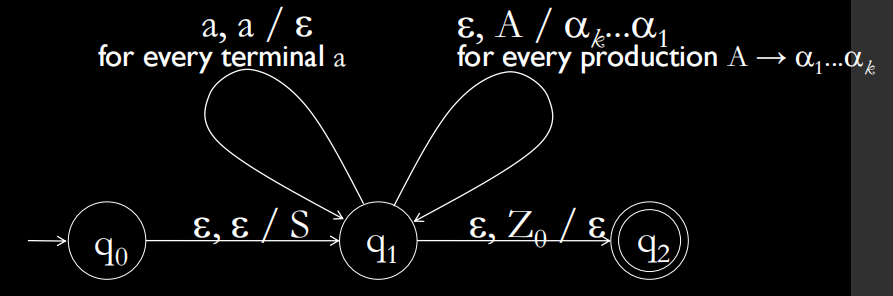
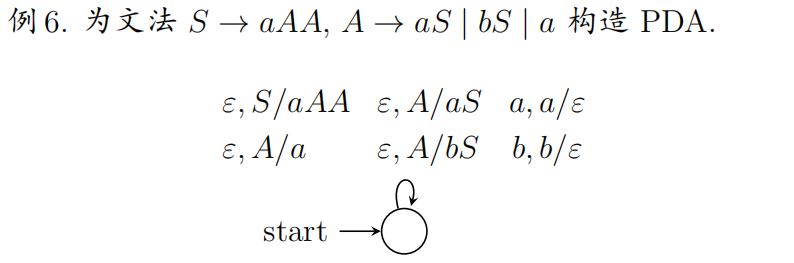
6.泵引理(RL/CFL)
6.1 RL的泵引理
用于证明一个语言不是正则语言,泵引理如下:
如果语言 L 是正则的*,* 那么存在正整数 $N$,对$\forall w\in L$,
只要$|w|≥N$, 就可以将 $w$ 分为三部分 $w=xyz$ 满足:
$|y|>0$
$|xy|≤N$
$\forall k\ge 0,xy^kz\in L$
- 采用”对抗赛“的方式证明,方便书写 下表中用$len(w)$表示$|w|$,因为markdown表格会识别’|‘符号…
证明$L_{01}=\lbrace 0^n1^n|n\ge 0\rbrace $不是正则语言
证明$L_{eq}=\lbrace w|w由数量相等的0和1构成\rbrace 不是正则的$
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^N1^N$,显然$w\in L,len(w)=2N>N$ |
| 选取$len(xy)\le N$,则$y=0^m$且$m\ge 1$ | 选取$i=2$,则$xy^2z=0^{N+m}1^N\not \in L_{01}(L_{eq})$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 0^i1^j|i>j\rbrace $不是正则的
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^{N+1}1^N$,显然$w\in L,len(w)=2N+1>N$ |
| 选取$len(xy)\le N$,则$y=0^m$且$m\ge 1$ | 选取$i=0$,则$xy^0z=0^{N+1-m}1^N\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace a^3b^nc^{n-3}|n\ge 3\rbrace $不是正则语言
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=a^{3}b^Nc^{N-3}$,显然$w\in L,len(w)=2N>N$ |
| 选取$len(xy)\le N$,则有三种情况:$y=a^m$或$y=b^m$或$y=a^lb^r$ | ①选取$i=2$,则$xy^2z=a^{3+m}b^Nc^{N-3}\not \in L$ .②选取$i=2$,则$xy^2z=a^3b^{N+m}c^{N-3}\not \in L$.③选取$i=2$,则$xy^2z=a^{3}b^{r}a^{l}b^{N}c^{N-3}\not \in L$ |
| 三种情况都不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 0^n10^n1|n\ge 0\rbrace $不是正则语言
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^{N}10^N1$,显然$w\in L,len(w)=2N+2>N$ |
| 选取$len(xy)\le N$,则$y=0^m$且$m\ge 1$ | 选取$i=0$,则$xy^0z=0^{N-m}10^N1\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 1^p|p是素数\rbrace $不是正则语言
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=1^{P},P$是大于$N$的最小素数,显然$w\in L,len(w)=P>N$ |
| 选取$len(xy)\le N$,则$y=1^b$且$b\ge 1,xyz=1^a1^b1^c$ | 选取$i=a+c$,则$xy^{a+c}z=1^{a+b(a+c)+c}=1^{(a+c)(1+b)}\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
判断$L=\lbrace 1^p|p能被3整除\rbrace $是否是正则的
$1^P$是正则的,$1^P=(111)^{*}$
以下为错误示范:$xy^{4b+1}z\not =1^{a+c+4b+1}$
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=1^{P},P$是大于$N$的最小的3的倍数,显然$w\in L,len(w)=P>N$ |
| 选取$len(xy)\le N$,则$y=1^b$且$b\ge 1,xyz=1^a1^b1^c$ | 选取$i=4b+1$,则$xy^{4b+1}z=1^{a+c+4b+1}$,由于$a+b+c=3k,k\in N^+$,因此$1^{a+c+4b+1}=1^{3(k+b)+1}\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 0^n|n是完全平方数\rbrace $不是正则的
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^{P},P$是大于$N$的最小的完全平方数,$P=K^2$,显然$w\in L,len(w)=P>N$ |
| 选取$len(xy)\le N$,则$y=0^b$且$b\ge 1,xyz=0^a0^b0^c$ | 选取$i=b+P$,则$xy^{b+P}z=0^{a+c+b+P}=0^{2P}=0^{2K^2}$,由于$2K^2$不是完全平方数,因此$xy^{b+P}z\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 0^n|n是完全立方数\rbrace $不是正则的
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^{P},P$是大于$N$的最小的完全立方数,$P=K^3$,显然$w\in L,len(w)=P>N$ |
| 选取$len(xy)\le N$,则$y=0^b$且$b\ge 1,xyz=0^a0^b0^c$ | 选取$i=b+P$,则$xy^{b+P}z=0^{a+c+b+P}=0^{2P}=0^{2K^3}$,由于$2K^3$不是完全平方数,因此$xy^{b+P}z\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
证明$L=\lbrace 0^n|n是2的幂\rbrace $不是正则的
| BOSS | Me |
|---|---|
| 选取$N\in Z^+$ | 选取$w=0^{P},P$是大于$N$的最小的2的幂次,$P=2^K$,显然$w\in L,len(w)=P>N$ |
| 选取$len(xy)\le N$,则$y=0^b$且$b\ge 1,xyz=0^a0^b0^c$ | 选取$i=2$,则$xy^2z=0^{P’}$,由于$P<P’\le P+N<2P$,$2P$是大于$P$的下一个2的幂次数字,因此$xy^{2}z\not \in L$ |
| 不满足泵引理,因此不是正则语言 |
6.2 CFL的泵引理
大概率不考…
如果语言$L$是$CFL$,存在正整数$N$,对$\forall z\in L$,只要$|z|\ge N$,就可以将$z$分为五部分$z=uvwxy$,满足
- $vx\not =\epsilon(|vx|>0)$
- $|vwx|\le N$
- $\forall i\ge 0,uv^iwx^iy\in L$
7.CNF/CYK算法
7.1 文法化简的顺序
-
消除$\epsilon -$产生式
$S\rightarrow AB$,$A\rightarrow AaA|\epsilon$,$B\rightarrow BbB|\epsilon$
A、B是可空的,因此$S\rightarrow AB|A|B$,$A\rightarrow AaA|Aa|aA|a$,$B\rightarrow BbB|Bb|bB|b$
-
消除单元产生式
若有$A\rightarrow B$,则称$[A,B]$为单元对,删除$A\rightarrow B$,然后将$B$的产生式复制给$A$
-
消除非产生的无用符号
$A\rightarrow \alpha$,且$\alpha$中符号都是产生的,则$A$是产生的
-
消除非可达的无用符号
$S$是可达的,$A\rightarrow \alpha$,且$A$是可达的,则$\alpha$中符号都是可达的
7.2 CNF化简算法
每个不带 $ε$ 的 CFL 都可以由这样的 CFG G 定义*,* G 中每个产生式的形式都为$A\rightarrow BC$ 或 $A\rightarrow a$
这里的 $A,B和C$ 是变元,$a$ 是终结符
转换方法:
-
将产生式$A\rightarrow X_1X_2…X_m$中的终结符$a$替换为新变元$C_a$
-
增加新产生式$C_a\rightarrow a$
-
引入新变元$D_1,D_2,…,D_{m-2}$,将产生式$A\rightarrow B_1B_2…B_m$替换为级联产生式 $$ A\rightarrow B_1D_1\ D_1\rightarrow B_2D_2 …\ D_{m-2}\rightarrow B_{m-1}B_{m} $$
将下面的CFG写成CNF
$S\rightarrow \epsilon | ADDA$
$A\rightarrow a$
$C\rightarrow c$
$D\rightarrow bCb$
$S’\rightarrow S|\epsilon$
$S\rightarrow AE$,$E\rightarrow DF$ ,$F\rightarrow DA$
$A\rightarrow a$ ,$B\rightarrow b$,$C\rightarrow c$
$D\rightarrow BG$,$G\rightarrow CB$
$CFG\ G=(\lbrace S,A,B\rbrace ,\lbrace a,b\rbrace ,P,S)$,产生式集合$P$为:
$S\rightarrow bA|aB$
$A\rightarrow bAA|aS|a$
$B\rightarrow aBB|bS|b$
请设计等价的$CNF$
$S\rightarrow C_bA|C_aB$,$C_b\rightarrow b$,$C_a\rightarrow a$
$A\rightarrow C_bD_1|C_bS|a$,$D_1\rightarrow AA$
$B\rightarrow C_aD_2|C_bS|b$,$D_2\rightarrow BB$
7.3 CYK成员性测试算法
CYK算法用来对CNF文法进行成员性测试,例子如下:$X_{ij}$代表第$i$个到第$j$个字母区间

举个例子,判断$X_{14}(bbab)$时,检查如下,其中$\times$代表笛卡尔积
- $X_{11}\times X_{24}=\lbrace BS,BC\rbrace $,在表中查找是否属于产生式,这里找到$S$产生BC
- $X_{12}\times X_{34}=\lbrace \rbrace $,空集跳过
- $X_{13}\times X_{44}=\lbrace AB\rbrace $,找到$S$和$C$都产生$AB$
因此答案$X_{14}=\lbrace S,C\rbrace $
8.构造图灵机
注意:画自动机时,可以先画出第一次循环,后面再补上循环缺失的转移
8.1 四则运算
加法、减法、乘法、乘方
加法
输入:$B000C00B$
输出:$B00000B$
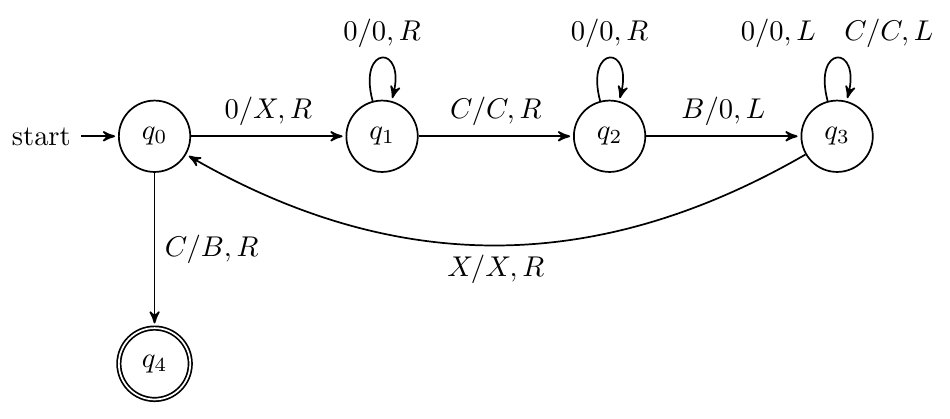
整数真减法
输入:$B000100B$ 输出:$B0B$
输入:$B00010000B$ 输出:$B$
这里采用1作为隔断,输出为前面的0数量-后面的0数量
以000100(3-2)为例,以初始的1为界限,我们不断采用将1左边最远的0标记为B,1右边最近的0标记为1的操作
直到
-
发现1右边没有0了(即跳过1后遇到B),说明满足$m\ge n$且$n$标记完了,此时我们1左边是多标记了一个0为B的
因此需要往左把标记的1变为B,只保留1前面的0,并且把最左边的一个B改为0(因为多标记了)
-
发现前缀0没有了,只剩下开始用来隔断的1,说明$m<n$,因此往右把所有的01转B即可
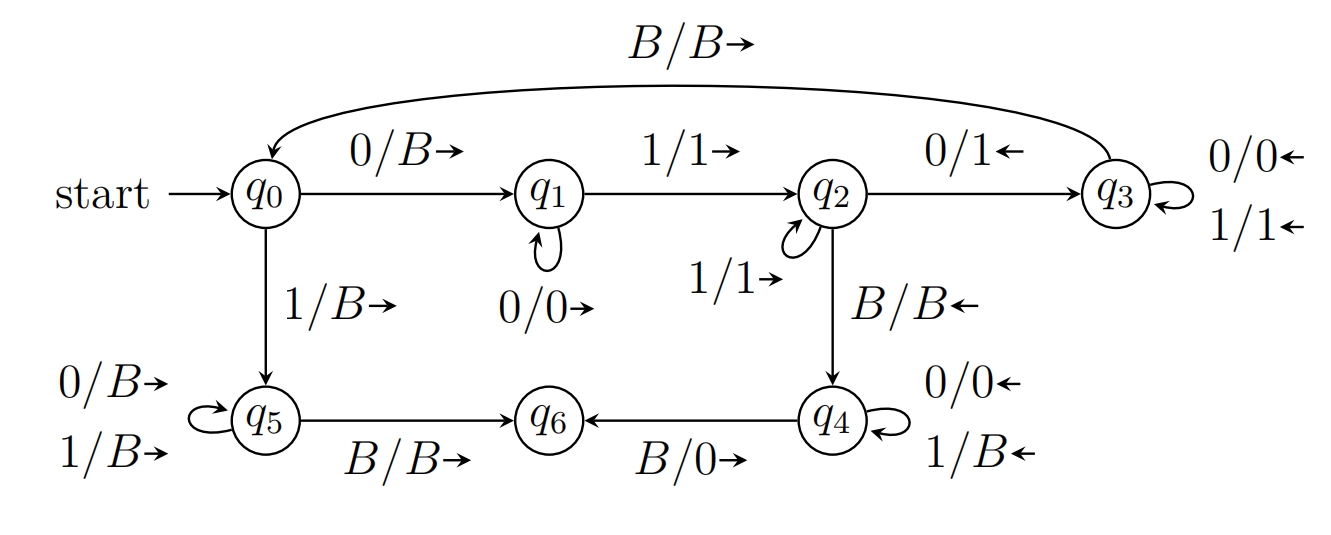
乘法
输入:$B000C00B$
输出:$B000000B$
太难了 建议抄在纸上T_T
- $q0$到$q3$将$B000C00B$变为$B000C00C$,并将新的字符串放在末尾的C后
- 思路:针对两个$C$之间的0,我们从左往右,每标记一个,就在末尾C后面复制开头B和中间C之间的0,即$q5$到$q10$实现转换为$BYYYCX0C000B$,$q5$到$q3$将前面的Y转换回来,准备下一轮的复制,即变为$B000CX0C000B$
- $q3$遇到末尾$C$则代表乘法完成,结果存放在末尾C后面,需要将末尾C和前面的C/X/0标记回B(即图中$q3$到$q12$,画的有点问题)
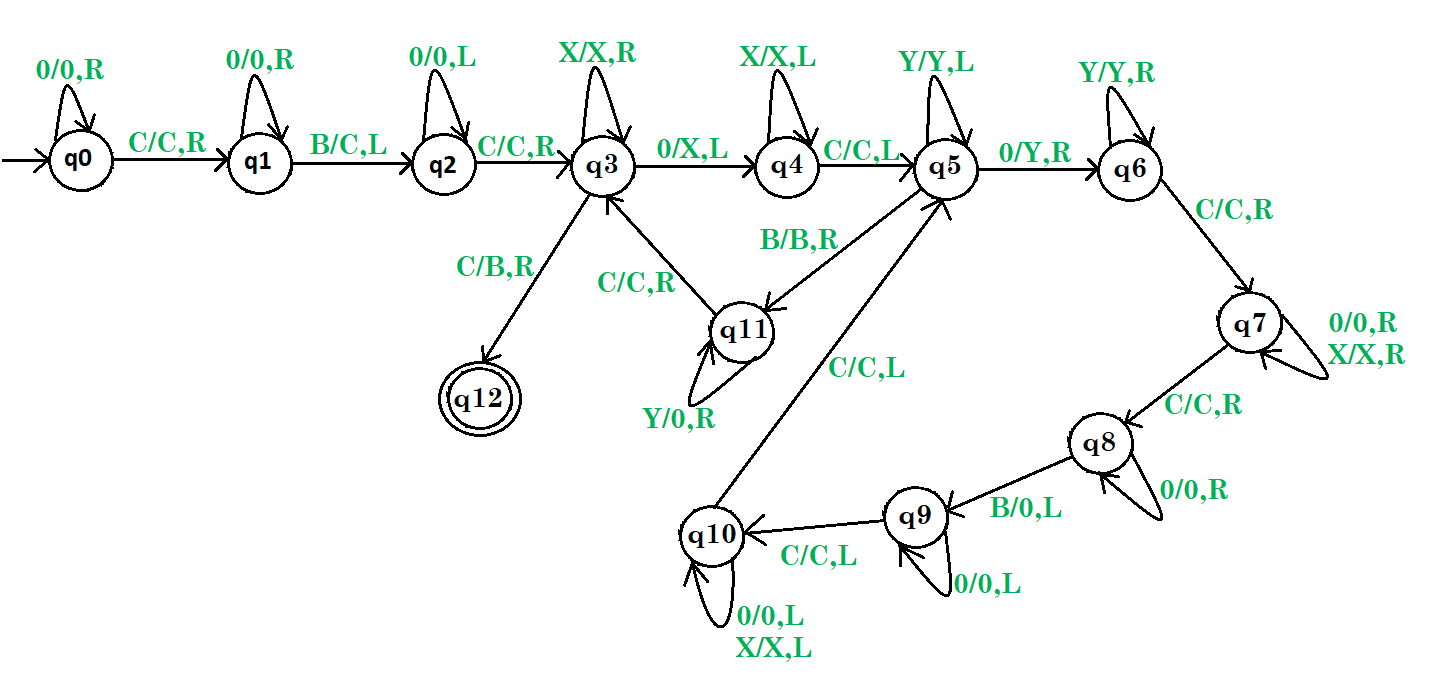
8.2 字符串操作
移动、复制、查找、反转
复制字符串:
输入:$B10110B$
输出:$B10110C10110B$
比较简单,分01讨论即可,最后别忘了把前面标记的01标记回去(不画图了^ _ ^,下图来源)

反转字符串
输入:$B10110B$
输出:$B01101B$
从右往左标记,分01讨论即可
8.3 特定排列
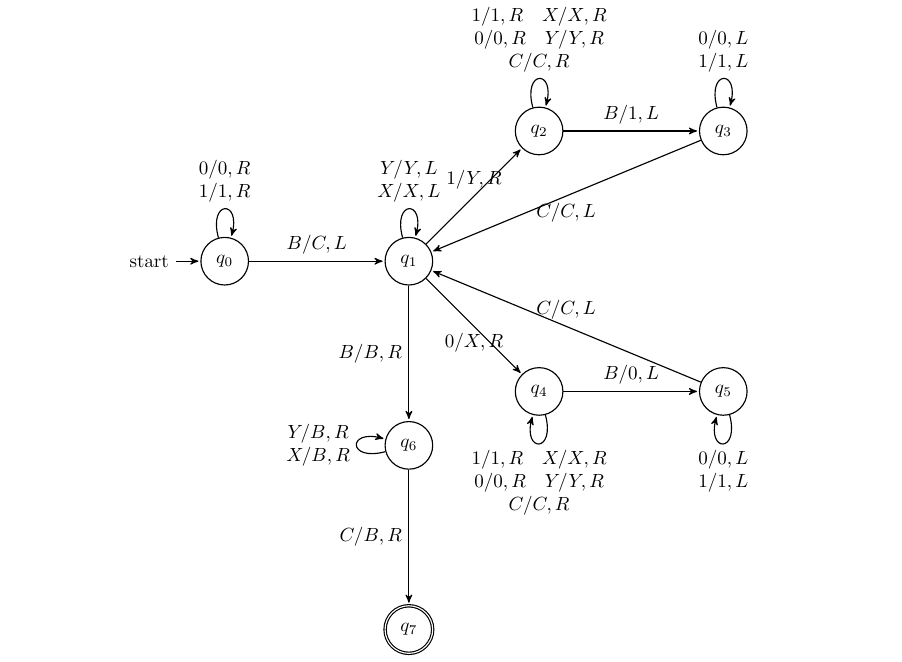
设计识别$\lbrace 0^n1^n|n\ge 1\rbrace $的图灵机
思路:我们找出每一对匹配的$0$和$1$,将其标记为$X$和$Y$,当所有都标记完成则接受该字符串
即$B000111B\rightarrow BX00Y11B\rightarrow BXX0YY1B\rightarrow BXXXYYYB$
建立循环如下,
- 识别到$0$,将其改为$X$并往右移动
- 跳过中间所有的$0$和$Y$(一直往右)
- 识别到$1$,改为$Y$往左移动
- 跳过中间所有的$Y$和$0$(一直往左)
- 找到$X$后往右移动,此时回到循环开头
如果在循环开头遇到$Y$,则说明$01$对已经标记完,则跳过所有的$Y$找到$B$,就进入了终结状态
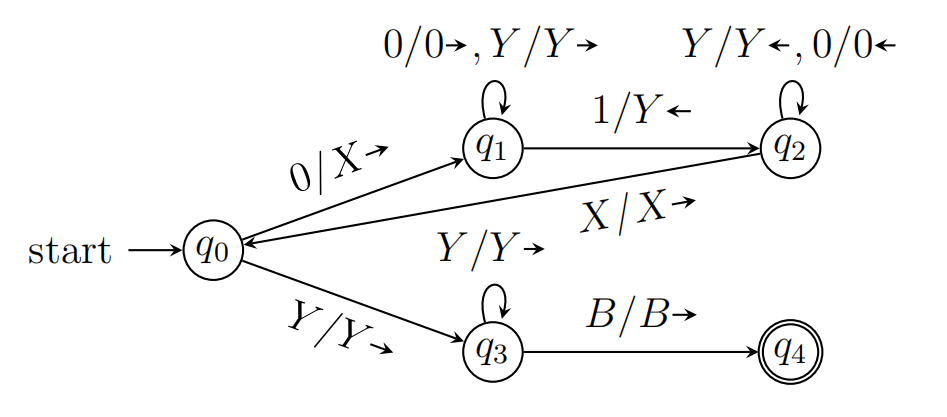
此图灵机接受$0011$的ID序列是? $$ \begin{aligned} q_00011&\ \vdash Xq_1011\ \vdash X0q_111\ \vdash Xq_20Y1\\ &\ \vdash q_2X0Y1\ \vdash Xq_00Y1\ \vdash XXq_1Y1\\ &\ \vdash XXYq_11\ \vdash XXq_2YY\ \vdash Xq_2XYY\\ &\ \vdash XXq_0YY\ \vdash XXYq_3Y\ \vdash XXYYq_3B\\ &\ \vdash XXYYBq_4B \end{aligned} $$
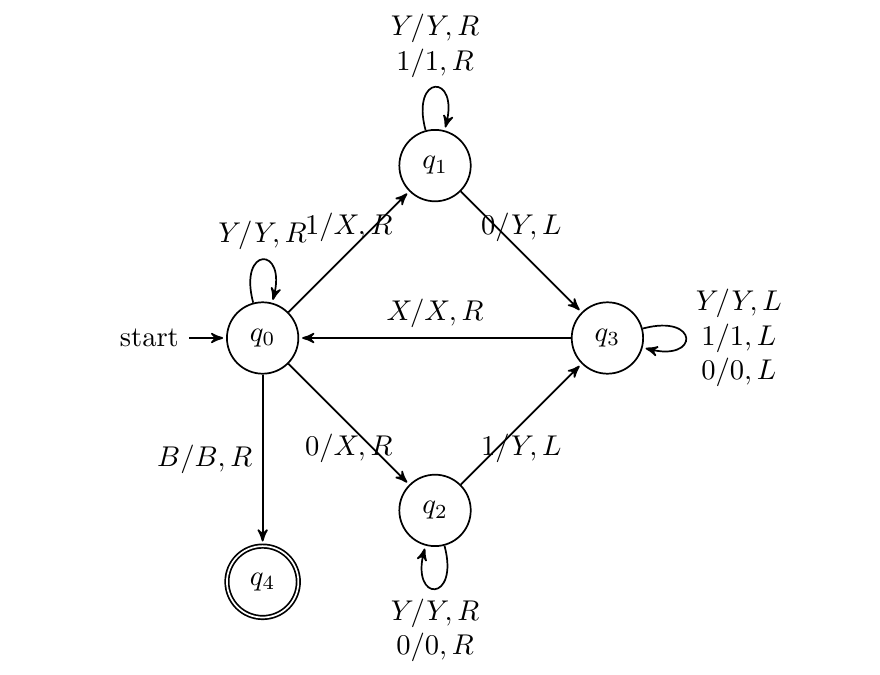
构造TM识别$L=\lbrace w\in \lbrace 0,1\rbrace ^{*}|w中01的数量相等\rbrace $
由于$w$中的01一定匹配,我们从左往右,不断找到一对01匹配项,对于左边的每个0/1,标记为为X,找到右边匹配的1/0标记为Y
因此最新的X(位于q0处,且是最左边的X)的左边一定都标记完成,右边一定只剩下Y;当跳过Y遇到B时,则接受该字符串
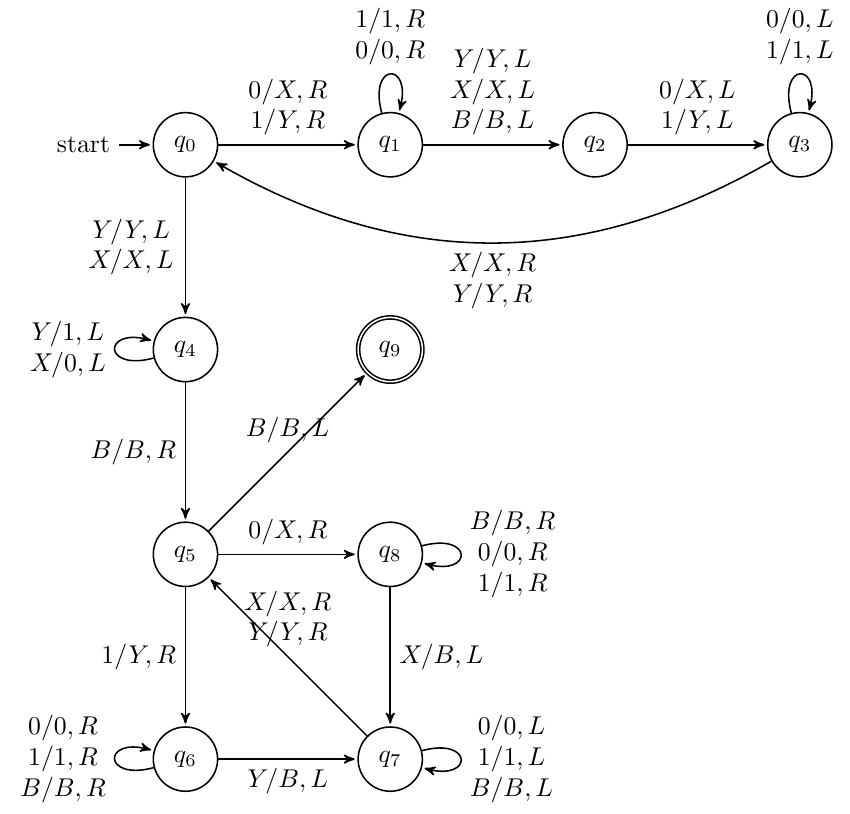
构造TM识别$L=\lbrace ww|w\in\lbrace 0,1\rbrace ^{*}\rbrace $
分为两步,以$B01110111B$作为例子,
-
找到中点:我们不断填充左边和右边,最终指针停在$BXYYY$$X$$YYYB$的位置
-
判断左边和右边:我们让指针左移一格,然后把左半边的XY还原为01,此时$B0111XYYYB$
然后不断标记左边,对右边进行判断即可,判断一个就标记为B。左边遇到B则进入终结状态
构造TM识别$L=\lbrace ww^R|w\in\lbrace 0,1\rbrace ^{*}\rbrace $
分01讨论即可,从两端往中间标记

构造TM识别语言$\lbrace a^nb^nc^n|n\ge 1\rbrace $
每标记一个a(a/X),就往右移动匹配一个b(b/Y),再往右移动匹配一个c(c/Z),然后往左直到X,再往右,开始重复以上步骤。
注意,当a识别完(X往右遇到Y)时,需要检查是否所有的b和c都转为了Y和Z,是则接收,否则不接收。
构造TM识别语言$\lbrace a^nb^mc^n|n\ge m\rbrace $,其中$n$和$m$为正整数
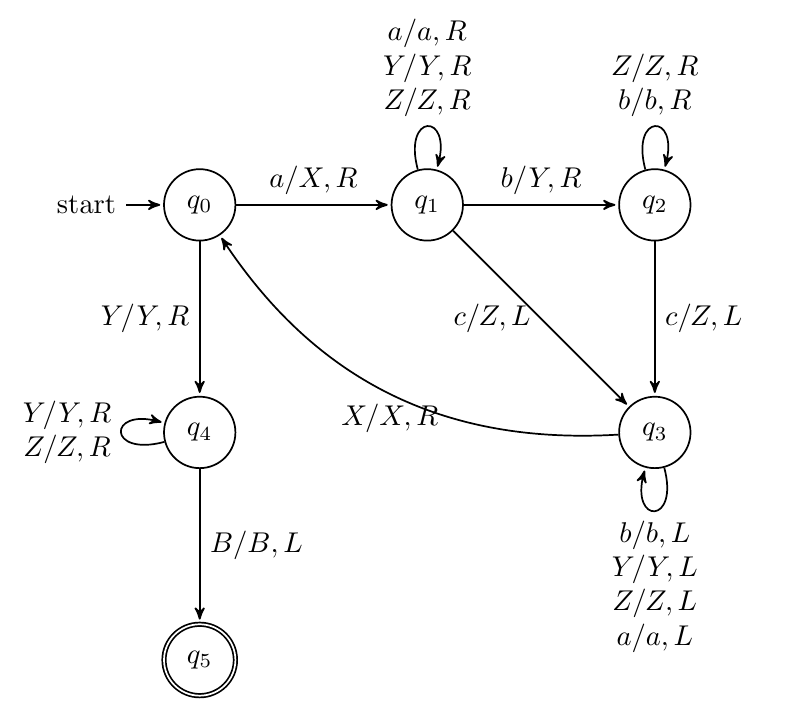
构造TM识别语言$\lbrace a^nb^ma^{n+m}\rbrace $,其中$n$和$m$为正整数
先查找a,再查找b,都标记右边的a即可

构造TM识别语言$\lbrace a^nb^{2n}\rbrace $,其中$n$为正整数
每个a匹配两个b即可(a/X,b/Y),直到a识别完(遇到左端的Y),需要检查b是否识别完(Y结束后就是B)
9.讨论
9.1 不可判定性undecidable
对于一个问题,如果存在一个算法能回答它,则该问题是可判定的,即“可判定问题”=“递归语言”;否则是不可判定的
-
不可判定的问题:
- 是否会执行程序中的特定代码行?
- 给定的无上下文语法是否无二义?
- 两个给定 CFG 生成相同的语言吗?
- ……
-
对角化语言$L_d$:不是递归可枚举语言,即不存在接受$L_d$的图灵机
-
通用语言$L_u=\lbrace M111w|w\in L(M)\rbrace $(图灵机$M$和输入串$w$的编码组成的有序对$(M,w)$):
递归可枚举(RE)但非递归的语言,即不可判定的
-
赖斯定理:令$L_P$为$TM\ M$的二进制$TM$代码,满足$L(M)$具有属性P。
有两个属性可以判定:
- 不包含任何RE语言(判定为假)
- 包含每个RE语言(判定为真)
对于其他属性$P$,$L_P$不可判定。
证明:采用归约的技术,将$L_u$归约到$L_P$,由于$L_u$不可判定,因此$L_P$不可判定